|
Kapitel Zwei:
Einfache mathematische Berechnungen und Manipulationen |
 |
|
|
|
Kapitel 1
|
|
Kapitel Zwei:
Einfache mathematische Berechnungen und Manipulationen |
 |
|
|
|
Kapitel 1
|
Bemerkung: Die Ausgabe der Werte erfolgt grundsätzlich im Bogenmaß (radians). Um sie in Gradwerte (degrees) umzuwandeln, müssen sie wie folgt umgerechnet werden:
> radians := Pi/2.;
> radians*180./Pi;
> degrees := %;
> radians := degrees*Pi/180;
oder mittels convert:
> restart: > convert(Pi/2, degrees);
> evalf(convert(%, radians));
> 3*4+5;
> 3*(4+5);
> 2^3^4; syntax error: 2^3^4; ^Mehrere aufeinanderfolgende Exponenten müssen bei der Hütchen-Schreibweise in Klammern gesetzt werden.
> 2^(3^4);
Ausmultiplizierung von Polynomen (expansion of polynomials):
> expand((x-2)^2);
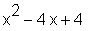
Faktorisierung (factoring)
> factor(%);
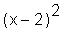
Vereinfachung (simplification)
> (x-1)^2+(x+4)^2;
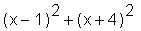
> simplify(%);
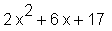
Zusammenfassung mittels collect in bezug auf eine bestimmte Variable (hier das zweite Argument):
> p := 5*x+a*x-a;
> collect(p, x);
> collect(p, a);
Auswahl der Teile eines Polynomes, die eine bestimmte 'Eigenschaft' besitzen:
> select(has, p, a);
has ist hierbei ein fester Bezeichner, der das Polynom p auf die Eigenschaft, ob es den Term a besitzt, untersucht. select zeigt die betreffenden Teile an.
Quadratische Ergänzung:
> restart: > p := x^2+2*x+2;
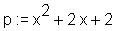
> with(student): > completesquare(p, x);
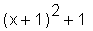
completesquare ist nicht Bestandteil der Standardbibliothek Maples, in welcher die fundamentalen Befehle und Funktionen gespeichert sind, sondern ist in einem sog. Paket (hier student) enthalten, welches Sie vor Nutzung der dort definierten Kommandos erst mit with(Paketname) aufrufen müssen, damit alle enthaltenen Befehle zur Verfügung stehen. Der Sinn des Konzeptes nachladbarer Pakete ist, den Arbeitsspeicherbedarf Maples so gering wie möglich zu halten, damit dieses Computeralgebrasystem auch auf 'kleineren' Computern arbeiten kann. Daher sind nur die meist genutzten Befehle sofort beim Start verfügbar, nicht aber spezielle. Mehr zur Konstruktion und Geschichte Maples finden Sie im Anhang.
Sortieren nach absteigendem Grad der Glieder eines Polynomes:
> restart: > poly := x^2-3*x^5+x;
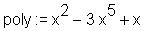
> sort(poly);
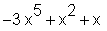
Auflistung aller Glieder des Polynomes mit op:
> glieder := op(poly);
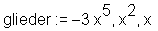
Herausgriff des n-ten Gliedes der Variable 'glieder', hier n=1:
> glieder[1];
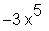
Man beachte die eckigen Klammern.
Koeffizient der höchsten Potenz (leading coefficient):
> lcoeff(poly);
Ermittlung aller Koeffizienten der Unbestimmten x in einem Ausdruck:
> coeffs(poly, x);
Grad (degree) des Polynomes:
> degree(poly);
Niedrigster Grad des Polynomes:
> ldegree(poly);
Ein Vergleich von Ausdrücken (expressions) geschieht durch die Operatoren
> u := 50: > if u=50 then > lprint(`richtig`) > else > lprint(`falsch`); > fi;richtig
Die oben erfolgte Eingabe erfolgt entweder in einer Zeile oder auf mehreren Zeilen, die durch Betätigung der Tasten SHIFT & RETURN voneinander getrennt werden, aber für Maple als eine Zeile erkannt werden.
Die if-Anweisung untersucht Bedingungen. Wenn (if) eine Bedingung (hier u=50) zutrifft, dann wird der then-Teil abgearbeitet, ansonsten (d.h. wenn die Bedingung nicht zutrifft) der else-Teil. Eine if-Anweisung muß generell mit einem fi abgeschlossen werden. Siehe auch: ?if.
Text wird durch lprint(`text`) oder mittels print(`text`) auf dem Bildschirm ausgegeben, hierbei muß der Text in sog. back quotes ` (ASCII Kontrollcode 96) eingeschlossen sein. Die Taste hierfür befindet sich rechts neben dem 'ß', das Zeichen wird folgendermaßen erzeugt: 1) Drücken der Shift-Taste zusammen mit der `-Taste, 2) Loslassen und 3) nachfolgendes Betätigen der Leertaste.
evalb(gleichung) untersucht (evaluates) eine Gleichung auf ihren Booleschen Wahrheitswert:
> evalb(u=50);
> evalb(u<50);
Definition einer Gleichung (equation):
> 4+x*3=y*sqrt(2);
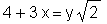
Zuweisung an eine Variable durch:
> eq1 := %;
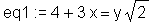
Ermittlung der linken (left-hand) und rechten Seite (right-hand side) der Gleichung:
> lhs(eq1);
> rhs(eq1);
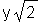
Auflösung der Gleichung nach der Variablen y durch isolate:
> readlib(isolate): > isolate(eq1, y);
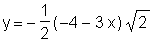
> simplify(%);
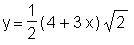
Der Befehl isolate steht nicht sofort zur Verfügung, Sie müssen ihn erst durch den besonderen Aufruf readlib(isolate) aktivieren.
Die Lösung von Gleichungen oder Gleichungssystemen geschieht mittels solve bzw. fsolve, letzteres für Fließkommalösungen; als erstes Argument wird die Gleichung und als zweites die Variable, nach der aufgelöst werden soll, angegeben.
> eq2 := 1/4*x^3-4*x=0;
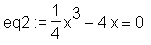
> solve(eq2, x);
> fsolve(eq2, x);
Achtung: Fließkommaberechnungen sind bei Maple wie bei allen Computerberechnungen nur Approximationen bzw. Näherungen. Besonders bei sehr großen Zahlen können sich leicht Fehler einschleichen. Hierbei empfiehlt sich das Heraufsetzen von Digits auf einen höheren Wert oder auch die Umwandlung eines Ausdruckes in einen rationalen Wert, welcher generell absolut genau ist. Siehe: convert/rational im Abschnitt 'Brüche' dieses Kapitels.
solve bzw. fsolve ermitteln nur bei Polynomen alle Lösungen.
Die Sinusfunktion hat unendlich viele Nullstellen.
> f := x -> sin(x);
(Es ist normal, daß das alleinige Argument 'x' der Sinus-Funktion, wie bei allen mathematischen Funktionen, nicht angezeigt wird.)
Wird ein Term (oder Funktion) als erstes Argument in solve bzw. fsolve eingesetzt, so kann dieses entweder in der Form 'Term=Zahlenwert' oder nur 'Term' geschehen. Im letzteren Falle wird dann der Term / die Funktion gleich Null gesetzt.
> solve(f(x), x);
Auch die Angabe des Intervalles (interval), z.B. [0, 10], in dem nach Nullstellen (zeros, x-intercept points) gesucht werden soll, führt hierbei nicht weiter:
> fsolve(f(x), x=0 .. 10);
aber bei Polynomen funktioniert es:
> fsolve(1/4*x^3-4*x, x=-1 .. 10);
Das math-Paket enthält die Funktion fnull, welche alle Nullstellen innerhalb eines bestimmten Intervalles auch bei periodischen Funktionen bestimmt.
assign bewirkt, daß eine durch solve ermittelte Lösungsmenge auch der entsprechenden Variable zugewiesen wird:
> equ := x+1;
> sol := solve(equ, {x});
> x;
Hier besitzt die Variable x noch nicht den Lösungswert -1.
> assign(sol); > x;
Berücksichtigen Sie bitte, daß die Variable x jetzt einen Wert trägt, also nicht mehr als Unbestimmte dienen kann. Wenn nötig, setzen Sie sie mit
zurück.
solve liefert, wenn vorhanden, immer auch komplexe Lösungen.
> restart: > equ := 2*x^4-2=-1;
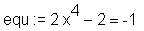
> solve(equ);
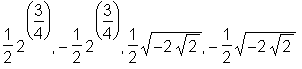
> evalf(%);
fsolve hingegen errechnet reelle Lösungen, mit der Option 'complex' können Sie aber neben den reellen auch komplexe Ergebnisse ermitteln lassen:
> fsolve(equ);
> fsolve(equ, x, complex);
Werden die Lösungen sehr umfangreich, so setzt Maple für mehrfach vorkommende Teilterme sog. 'Labels' der Form %n ein, so daß das Ergebnis etwas übersichtlicher wird.
> k := x -> x^3+x^2;
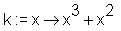
> solve(k(x)=1);
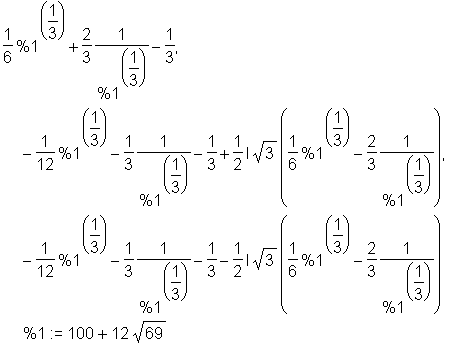
Bei solchen ausufernden Lösungstermen empfielt es sich, die Ergebnisse als Liste in einer Variablen zwischenzuspeichern, um auf die einzelnen Resultate über ihren Index zugreifen zu können. Zur Abspeicherung in eine Liste setzen Sie den solve-Befehl in eckige Klammern [ ]. Bei einem Index-Zugriff tritt das Label nicht mehr auf, es wird die komplette Lösung angezeigt. (Auf die komplette Maple-Ausgabe wird in den folgenden Beispielen verzichtet.)
> loesung := [solve(k(x)=1)];
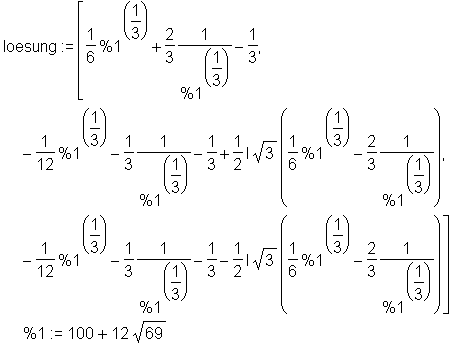
Erste Lösung:
> loesung[1];
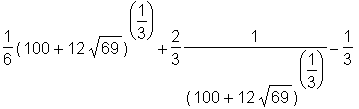
Durch Verwendung einer for-Schleife lassen sich alle Lösungen anzeigen. Mit nops ermittelt man die totale Anzahl der Einträge in die Liste.
> for i to nops(loesung) do > loesung[i] > od; ...Mit interface(labelling=false); weisen Sie Maple V an, Labels nicht zu verwenden und statt dessen die Ausgabe ungekürzt zu vollziehen. Durch interface(labelling=true); können Sie diese Einstellung wieder rückgängig machen. Ein restart bewirkt dieses nicht.
Bei Polynomen mit einem Grad größer oder gleich 5 findet solve in den meisten Fällen keine expliziten Lösungen. Es wird dann die RootOf- Darstellung benutzt.
> k := x -> x^5+x^4;
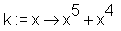
> solve(k(x)=1);
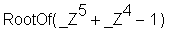
Die numerischen Lösungen lassen sich aber mit allvalues berechnen.
> allvalues(");
In einigen Fällen gelingt durch Setzen der Umgebungsvariablen _EnvExplicit auf den Wert true eine symbolische Berechnung:
> _EnvExplicit := true:
> y := 2*x-5;
> solve(y<3, x);
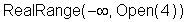
Release 4 und 5 benutzen standardmäßig statt der aus der mathematischen Literatur gewohnten Mengenschreibweise (s.o.) die 'RealRange'-Darstellung. Das obige Ergebnis sagt aus, daß das offene Intervall (-Unendlich, 4) die Ungleichung erfüllt. Durch Setzen des zweiten Argumentes, also 'x', in geschweifte Klammern wird das Ergebnis inb der aus Release 3 bekannten Mengenschreibweise ausgegeben:
> solve(y<3, {x});
Wie bei einfachen Gleichungen kann auch isolate die Ungleichung lösen.
> readlib(isolate): > isolate(y<3, x);
Sind zwei Punkte P1(x1, x2) und P2(x2, y2) gegeben, so läßt sich daraus die Geradengleichung y=mx+n ermitteln.
> restart: > with(student): > gl := y = m*x+n;
Die Steigung der Geraden wird mit dem Befehl slope aus dem Paket 'student' berechnet:
> m := slope([x1, y1], [x2, y2]);
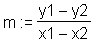
Der y-Achsenabschnitt n wird mit der zugegebenermaßen hier etwas kryptischen Anweisung
> assign(isolate(subs(x=x1, y=y1, gl), n)); > n := n;
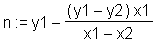
gefunden. subs setzt in der Gleichung gl für die dort enthaltenen Unbestimmten x und y jeweils x1 und y1 ein, danach wird mit isolate die Gleichung gl nach n aufgelöst und mit assign das Ergebnis der Variablen n zugewiesen. Für die nächsten Anweisungen muß n gelöscht werden.
> n := 'n':Ein konkretes Beispiel: Gegeben seien die Punkte (1, 5) und (2, 9). Die Punkte werden in eckigen Klammern gefaßt dem Befehl slope als Argument übergeben.
> m := slope([1, 5], [2, 9]);
Die Koordinaten eines Punktes werden jetzt in die Gleichung für x und y eingesetzt. Man beachte, daß der Wert für die Steigung m bereits in die Gleichung von Maple eingesetzt wurde. Die obige allgemeine Anweisung zur Ermittlung von n wird jetzt auseinandergezogen und auf mehrere Zeilen verteilt.
> subs(x=1, y=5 , gl);
> isolate(", n);
> assign(%); > gl;
Fertig !
Schnittpunkte einer Geraden mit den Koordinatenachsen oder zwischen zwei Geraden können Sie mit intercept berechnen, welches ebenfalls im Paket 'student' enthalten ist. Es hat im ungefähren dieselbe Funktion wie solve, wobei letzteres aber universeller einsetzbar ist.
Schnittpunkt mit der y-Achse:
> intercept(gl);
Schnittpunkt mit der vertikalen Gerade x=2:
> intercept(gl, x=2);
Schnittpunkt mit der Abszisse:
> intercept(gl, y=0);
Schnittpunkt zweier Geraden gl und z:
> z := y=x-2;
> intercept(gl, z);
> restart:
> solve({3*x-2*y=8, 5*x-3*y=4}, {x, y});
Die einzelnen Gleichungen können auch Variablen zugewiesen werden, welche dann in solve eingesetzt werden.
> gl1 := -2*x+2*y+7*z = 0;
> gl2 := x-y-3*z = 1;
> gl3 := 3*x+2*y+2*z = 5;
> solve({gl1, gl2, gl3}, {x, y, z});
Eine weitere Variation:
> gl_systeme := {gl1, gl2, gl3};
> gl_variablen := {x, y, z};
> solve(gl_systeme, gl_variablen);
Die Reihenfolge der einzelnen Lösungen erfolgt willkürlich. Die einzelnen Werte können wie bei einfachen Gleichungen mit assign den jeweiligen Variablen zugewiesen werden.
> assign(");
> x, y, z;
Auch die Lösung von Systemen, bei denen die Anzahl der Unbekannten ungleich der der Gleichungen ist, beherrscht solve.
> restart:
> solve({x-y+z=4, 2*x+3*y-z=-1}, {x, y, z});
Gegeben sei folgendes gebrochen-rationale Polynom:
> restart: > f := x->(0.5*x^3-1.5*x+1)/(x^2+3*x+2);
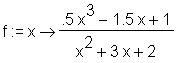
Die Division erfolgt durch Einsatz von convert/confrac; das erste Argument von convert ist das gebrochen-rationale Polynom selbst, das zweite die Option confrac, welche die Art der Division bestimmt, und das dritte Argument die im Polynom enthaltene Unbestimmte.
> bruch:=convert(f(x), confrac, x);
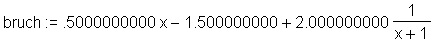
Umwandlung des Fließkommaausdruckes in einen rationalen Term:
> convert(bruch, rational);
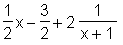
Bestimmung des Zählers (numerator):
> fz := numer(f(x));
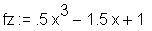
Bestimmung des Nenners (denominator):
> fn := denom(f(x));
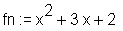
Ermittlung des Quotienten bei einer Division von Polynomen:
> qu := quo(fz, fn, x);
Ermittlung des Restes (remainder):
> re := rem(fz, fn, x);
> convert(qu, rational);
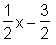
> convert(re, rational);
Zuweisung des Quotienten an eine neue Funktion mittels unapply:
> asymptote := unapply(%%, x);
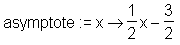
Hierbei wird als erster Parameter der zuzuweisende Ausdruck angegeben und als zweites das Argument (oder die Argumente) der neuen Funktion. Man ist oft versucht, eine unapply-Funktion mittels der Pfeilnotation zu definieren:
> func := x -> unapply(ausdruck, x);Richtig aber ist nur die Syntax:
> func := unapply(ausdruck, x);
> y := 3/x+4/x^2;
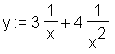
normal faßt nicht-gleichnamige Brüche zusammen (gemeinsamer Hauptnenner: common denominator):
> normal(y);
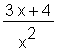
Partialbruchzerlegung (partial fractions):
> partialbruch := (x^2-3)/(x^3-x);
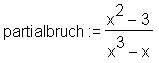
> convert(partialbruch, parfrac, x);
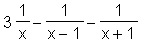
'Echte' Teilbarkeit von Polynomen. divide bestimmt, ob die beiden angegebenen Polynome ohne Rest teilbar sind. Wenn ja, so wird 'true' ausgegeben und das Ergebnis dem dritten Parameter übergeben:
> divide(x^3-2*x^2-5*x+6, x-1, sol1);
> sol1;
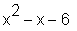
> divide(0.5*x^3-1.5*x+1, x^2+3*x+2, sol2);
> sol2;
MAPLE EINFÜHRUNG - MPLINTRO 04.00a vom 14. Dezember 1998
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/m2.htm