|
Kapitel Drei:
Graphiken |
 |
|
|
|
Kapitel 2
|
|
Kapitel Drei:
Graphiken |
 |
|
|
|
Kapitel 2
|
Die sog. Plotfunktionen ermöglichen eine vielseitige, wenn auch manchmal komplizierte graphische Darstellungen von Funktionen im zwei- und dreidimensionalen Raum.
> f := (x) -> (0.5*x^3-1.5*x+1) / (x^2+3*x+2):sowie deren Asymptote
> a := x -> 1/2*x-3/2:im Intervall [-5, +5]:
> plot(f(x), x=-5 .. 5);
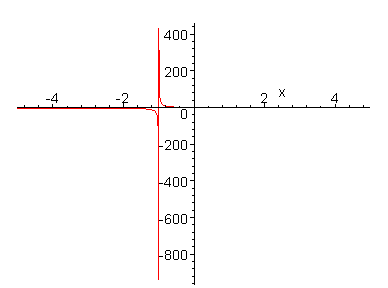
Wenn Sie in den Graphen mit der Maus klicken, so ändert sich die Kontextleiste. Durch Klicken auf die dortigen Icons können Sie die Graphen manipulieren, bessere Gestaltungsmöglichkeiten ergeben sich allerdings nur durch entsprechende Steuerung in der Kommandozeile (s.u.).
Als nächstes folgt der Ausdruck zweier Graphen in einem Fenster, wobei als dritter Parameter noch das y-Achsenintervall angegeben wird. Fehlt er, so bestimmt Maple V die Anpassung des Ordinatenbereiches selbständig.
Wenn mehr als eine Funktion angezeigt werden soll, müssen diese Funktionen entweder in geschweifte Klammern { }, (curly brackets) - also als Menge - oder als Liste in eckigen Klammern - getrennt durch Kommata, eingegeben werden. Verwenden Sie dann eine Liste, wenn Sie die Reihenfolge der Darstellung der Graphen genau steuern möchten (gegenseitige Überlagerungen).
Es fällt auf, daß beim obigen Graphen an der Unstetigkeitsstelle x=-1 eine vertikale Gerade gezogen wird. Dies können Sie (meistens) mit der Option discont=true beheben. Durch Angabe der Option scaling=constrained besitzen die x- und y-Achsen eine einheitliche Skalierung:
> plot({f(x), a(x)}, x=-10 .. 10, y=-10 .. 10,
scaling=constrained, discont=true);
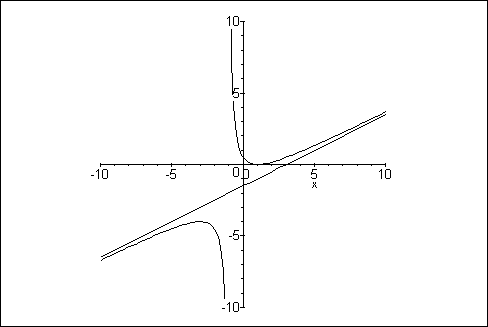
Bezeichnungen und Überschriften lassen sich ebenfalls eintragen:
> restart:
> with(plots):
> f := x -> x^(2/3):
> g := x -> x^(-1/2):
> text1 := textplot([8, f(8), `f(x) = x^(2/3)`], color=red,
align={BELOW, RIGHT}):
> text2 := textplot([8, g(8), `g(x) = x^(-1/2)`],
align={ABOVE, RIGHT}):
> graph := plot({f(x), g(x)}, x=-1 .. 10, y=-5 .. 5,
scaling=constrained, titlefont=[TIMES, BOLD, 11]):
> display({graph, text1, text2},
title=`Potenzen mit rationalem Exponenten`);
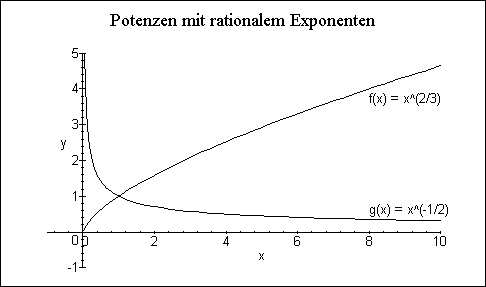
Nähere Erläuterung:
Die Anzeige des Graphen selbst sowie des Textes erfolgt nicht direkt, sondern durch Zuweisung an Variablen. Hierbei ist wichtig, daß die Befehle mit Doppelpunkt beendet werden, da ansonsten seitenlange Maple-interne Codes zur Darstellung der Kommandos im Arbeitsblatt ausgedruckt werden.
textplot dient der Anzeige von Texten innerhalb des Graphen, die Koordinaten sowie der Text an sich müssen von eckigen Klammern begrenzt sein. Die allgemeine Syntax dieses Befehles lautet:
Da mit der bloßen Angabe der Koordinaten der Text den Graphen meist überdeckt - wenn als y-Koordinate ein Funktionswert des Graphen genannt ist - erlaubt die Option align eine nähere Spezifizierung der Positionierung des Textes: ober- (ABOVE) oder unterhalb (BELOW) des Koordinatenpaares, rechts (RIGHT) oder links (LEFT) von ihm. Dennoch kommt es öfters vor, daß Text in die Kurve hineingeschrieben wird, hier können Sie nur manuell die Koordinaten nachkorrigieren. Die Positionsangaben von align müssen in geschweifte Klammern gesetzt werden.
Die Plotkommandos, welche den Variablen text1, text2 und graph zugewiesen wurden, werden durch display({variablen}) in einem Fenster zur Anzeige gebracht. Sowohl textplot als auch display erfordern die vorherige Initialisierung (der Kurzformen der Befehle) des Paketes 'plots' mit with(plots). Einzelne Befehle aus den verschiedenen Paketen können Sie aber auch direkt - ohne Verwendung von with - mit 'paket[befehl](Argumente)' nutzen, beispielsweise: 'plots[display]({graph, text1, text2}...)'.
Die sogenannten Plotoptionen, welche in den oberen Beispielen hinter dem x- bzw. y-Achsenbereich des plot-Befehles eingetragen wurden (wie z.B. 'scaling=constrained'), können auch voreingestellt werden, so daß diese für alle Plots einer Arbeitssitzung gelten und nicht immer wieder hinzugefügt werden müssen:
> restart: with(plots): > setoptions(scaling=constrained, axes=frame);Diese beiden Einstellungen bewirken eine Ausgabe des Graphen immer im Verhältnis 1:1 sowie die Darstellung der Achsen nicht mehr als Kreuz sondern als äußerer Rahmen. Weitere Einstellungen für die Koordinatenachsen sind:
> liste := [ [1, 1], [2, 2], [3, 1] ]: > plot(liste, x=0 .. 4, y=0 .. 3);Der letzte Punkt [3, 1] z.B. wird bei x=3 und y=1 gesetzt.
Es lassen sich dem Befehl plot verschiedenste Optionen mitteilen, die ein Anwender wählen kann, um den Graph seinen Wünschen gemäß zu gestalten. Sollen die Punkte nicht mit Linien verbunden werden, so unterdrückt die Einstellung 'style=point' dieses. Für die Darstellung der Punkte können verschiedene Symbole angegeben werden, z.B. ein Diamant (bzw. eine Raute).
> plot(liste, x=0 .. 4, y=0 .. 3, > style=point, symbol=diamond);Stiloptionen für zweidimensionale Plots sind:
Die Linienarten geben die Art der Strichelung der Kurven an, für n=0 und 1 ist die Linie komplett zusammenhängend bzw. durchgezogen, weitere positive Werte von n bestimmen andere Strichelungen. Zur Angabe der Linienart wird die Option linestyle verwendet.
Die Farben werden hier in eine Liste namens 'farben' eingetragen, man kann auf sie über einen Index (hier n) zugreifen. Die Linienart wird über den Befehl seq und den durch ihn ermittelten Wert für n gesteuert. Mehr zu seq und Listen siehe im Abschnitt 'Folgen natürlicher Zahlen' im Kapitel 4.
> farben := [red, navy, black, brown, gray]:
> graph := seq(plot(sin(x*n), x=-2 .. 2, linestyle=n,
> color=farben[n]), n=1 .. 5):
> display({graph}, axes=box);
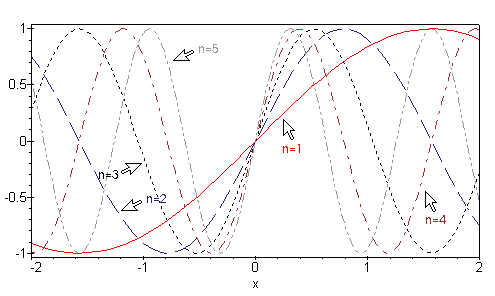
Für weitere Optionen siehe ?plot[options].
> restart: > with(student): > f := x -> sin(x): > showtangent(f(x), x=0.5, x=-2 .. 2);
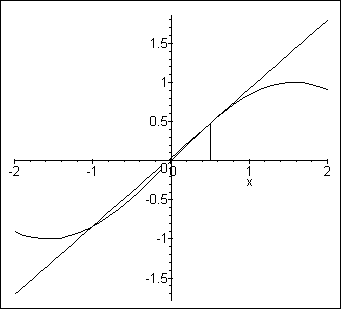
> restart: > with(plots): > eq1 := y=1/4*x^3-4*x;
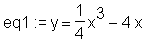
> eq2 := subs({y=x, x=y}, eq1);
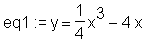
Mit subs({y=x, x=y}, eq1) werden die Variablen x und y in Gleichung eq1 miteinander vertauscht und der neue Term dem Bezeichner eq2 zugewiesen.
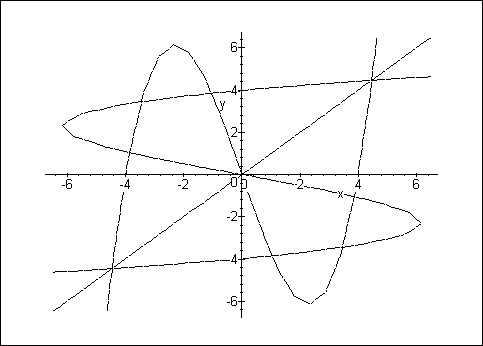
> implicitplot({eq1, eq2, y=x},
> x=-6.5 .. 6.5, y=-6.5 .. 6.5);
> with(plots):
> inequal({ x+0.25*y > 0, x-y <= 2}, x=-1 .. 4, y=-3 .. 3,
> optionsexcluded=(color=white),
> optionsopen=(color=navy, thickness=2),
> optionsclosed=(color=maroon, thickness=2),
> optionsfeasible=(color=gray),
> axes=frame, scaling=unconstrained);
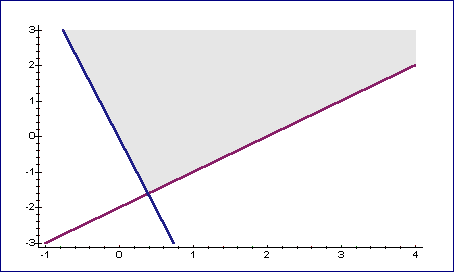
Horizontale und Vertikale können ebenfalls dargestellt werden:
> mondrian := {x > 1, y > 1, x < 2.5, x >= 1.4, y < 2};
> inequal(mondrian, x=0.5 .. 5, y=0 .. 5,
> optionsexcluded=(color=white),
> optionsopen=(color=black, thickness=3),
> optionsclosed=(color=gray, thickness=3),
> optionsfeasible=(color=maroon),
> axes=box, scaling=constrained);
Hinweis: Mit inequal können nur lineare Gleichungen bzw. Ungleichungen
bearbeitet werden, Polynome eines höheren Grades als 1 werden abgewiesen.
> with(plots): > f := (x, n) -> sin(n*x)*exp(-x): > animate(f(x, n), x=-3 .. 3, n=1 .. 20, frames=20);Mit dem optionalen Parameter frames bestimmen Sie die Anzahl der zu erstellenden Einzelbilder der Animation.
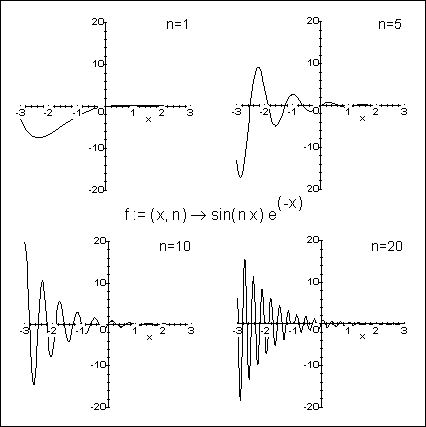
Maple ändert auch hier die Kontextleiste und zeigt verschiedene Schaltflächen zur Steuerung der Animation an:
> with(plots): > r := (x, y) -> exp(x)*sin(y): > plot3d(r(x, y), x=-4 .. 4, y=4 ..10);
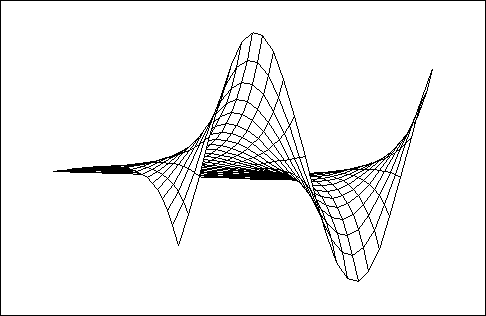
Wie bei zweidimensionalen Graphen lassen sich auch hier Optionen angeben:
> plot3d(r(x, y), x=0 .. 10, y=4 .. 10, > orientation=[64, 87], style=patchnogrid, > ambientlight=[1, 0.0, 0.9], shading=zhue, > grid=[100, 100]);orientation bestimmt den Blickwinkel in Grad, in der Reihenfolge horizontale und vertikale Richtung. Alternativ können Sie aber direkt mit der Maus den Graphen beliebig drehen und ihn sich so von den verschiedensten Seiten ansehen. Klicken Sie dazu mit der linken Maustaste auf den Graphen und bewegen Sie die Maus. Der Blickwinkel in der Statusleiste des Plotfensters wird kontinuierlich aktualisiert. 'Theta' gibt den horizontalen und 'Phi' den vertikalen Blickwinkel an.
Haben Sie nun 'Ihre' bevorzugte Perspektive gefunden, so können Sie die Werte der Winkel in die Option orientation übernehmen.
style definiert die Art der Darstellung, hier 'patchnogrid'. Stile sind:
> plot3d(r(x, y), x=0 .. 10, y=4 .. 10, orientation=[64, 87], > grid=[50, 50], shading=none, color=navy); > plot3d(r(x, y), x=0 .. 10, y=4 .. 10, orientation=[64, 87], > grid=[50, 50], shading=none, color=sin(x)*cos(y));Wird die Farboption angegeben, so erfolgt die Ausgabe automatisch im Stil 'patch'. Dieses kann aber durch Angabe eines (anderen) Stiles vermieden werden.
Die Mandelbrotmenge:
> with(plots); > mandelbrot := proc(x, y) > local z, m; > z:=evalf(x+y*I); > m:=0; > to 25 while abs(z)<2 do > z:=z^2+(x+y*I); > m:=m+1; > od; > m; > end: > plot3d(mandelbrot, -2 .. 0.5, -1.2 .. 1.2, grid=[50, 50]);
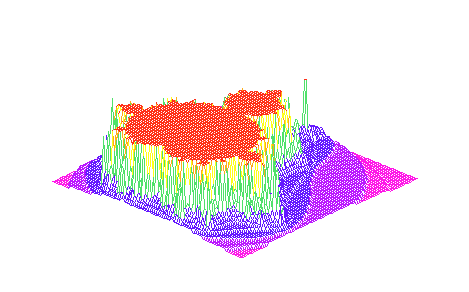
Zweidimensionale Darstellung eines 3D-Plots:
> plot3d(0, -2 .. 0.7, -1.2 .. 1.2, orientation=[-90,0], > grid=[250, 250], style=patchnogrid, scaling=constrained, > color=mandelbrot);Die eigentliche Struktur erhält der Graph durch die Einfärbung mittels color, welches die Prozedur- in Farbwerte umwandelt.
Die Mandelbrotprozedur entstammt dem Buch Maple V Programming Guide von M.B. Monagan, K.O. Geddes, G. Labahn & S. Vorkoetter (Waterloo Maple), Springer-Verlag.
> restart: with(plots): > spacecurve([t*cos(t), t*cos(t), t], t=0 .. 6*Pi, > orientation=[65, 81], axes=normal, shading=z);
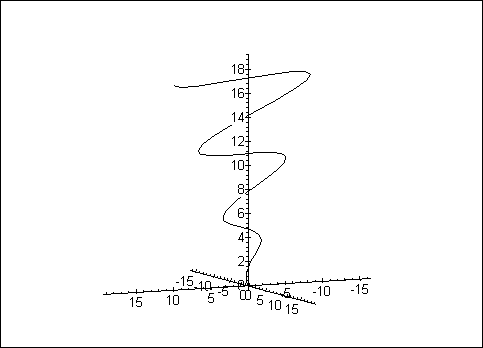
Eine andere Gestaltungsmöglichkeit des Ausgabe gestattet seq. Im Beispiel unten werden die Graphen der parametrischen Funktion f(x, t) nebeneinander für t von 1 bis 6 und den angegebenen Definitionsbereich von x im Raum gezeichnet. Beachten Sie die unterschiedlichen runden, geschweiften und eckigen Klammern.
> restart: with(plots):
> f := (x, t) -> t*x*exp(-x^2+1):
> spacecurve(
> { seq( [x, t, f(x, t), x=-5 .. 5], t=1 .. 6 ) },
> orientation=[-102, 82], shading=z, axes=frame);
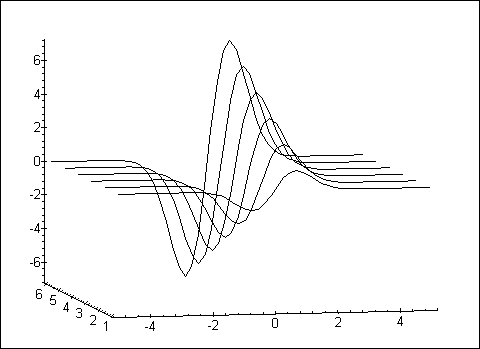
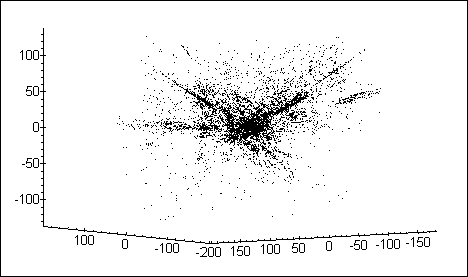
Auch Punkte, deren Koordinaten in einer Liste von Listen der Form
erfaßt sind, können mit pointplot dreidimensional skizziert werden. Im folgenden Beispiel wurden die Daten aus einer ASCII-Datei eingelesen und der Variablen g zugewiesen. Der Graph zeigt hier ca. 8.000 Galaxien im Umkreis von 200 Megaparsec (Mpc) mit unserer Milchstraße im Mittelpunkt. (1 Mpc sind 3.261.600 Lichtjahre.)
> pointplot(g, symbol=POINT, color=navy, > orientation=[156, 85], axes=FRAME, scaling=constrained);
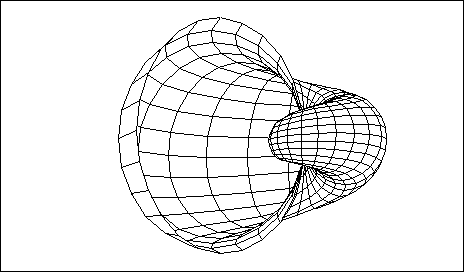
> sphereplot(1, x=0 .. 2*Pi, y=0 .. Pi, scaling=constrained, > style=hidden, orientation=[11, 73], color=navy); > sphereplot((1.3)^x*sin(y), x=-1 .. 2*Pi, y=0 .. Pi, > style=hidden, color=x, orientation=[61, 97]);
> with(plots): > interface(plotdevice=gif, plotoutput=`flaeche.gif`, > plotoptions=`width=800,height=600`);Mit der interface-Anweisung nehmen Sie die Umleitung vor. Die Option plotdevice definiert das Dateiformat; vorhanden sind u.a.:
| Format | R3 | R4 | R5 | Erklärung |
| bmp | ja | nein | nein | MS Windows BMP-Format |
| gif | ja | nein | ja | CompuServe Graphics Interchange Format 87a |
| jpeg | nein | ja | ja | Joint Picture Experts Group-Format |
| pcx | ja | ja | ja | ZSoft PCX-Format |
| tiff | ja | ja | nein | Tag Image File Format |
Beim JPEG-Format ist zu beachten, daß diese Bilder unter Informationsverlust komprimiert werden (mit ca. 87 %), dennoch weisen sie eine gute Qualität auf. Durch Release 3 erstellte Bilddateien haben einen schwarzen, mit Release 4 und 5 erstellte Graphiken einen weißen Hintergrund. Weitere Dateiformate sind unter ?plot[device] aufgelistet.
plotoutput gibt den Namen der zu speichernden Dateien an. plotoptions definiert die Auflösung des Bildes in Pixel mit 'width' (Breite) und 'height' (Höhe). Es darf in dem String kein Leerzeichen vorhanden sein.
Das Bild erstellen Sie auf die übliche Art.
> plot3d(sin(x)*exp(y), x=0 .. 10, y=4 .. 10, usw.);Mit
> interface(plotdevice=win);wird die Bildschirmdarstellung der folgenden Plots wieder eingeschaltet. Arbeiten Sie unter X Windows geben Sie statt win den Terminus X11 bzw. bei Apple Macintosh mac ein.
MAPLE EINFÜHRUNG - MPLINTRO 04.00a vom 14. Dezember 1998
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/m3.htm