| Kapitel Eins: Grundlagen |
 |
|
|
|
Einleitung
|
| Kapitel Eins: Grundlagen |
 |
|
|
|
Einleitung
|
Das Arbeitsblatt besteht i.d.R. aus drei Bereichen (auch Regionen genannt): Eingabebereich, Textbereich und Ausgabebereich. Im Eingabebereich werden die Rechenkommandos in Kommandozeilen erfaßt; in die Textregion können Sie Kommentare eintragen; in der Ausgaberegion erscheint das Ergebnis. Darüber hinaus gibt es auch noch die Graphikregion, in der die von Maple erzeugten Graphiken plaziert werden können.
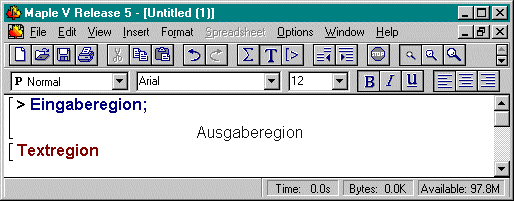
Diese Bereiche sind allerdings keine fixen Bildschirmregionen. Auf die Kommandozeile(n) in der Eingaberegion folgt die korrespondierende Ausgabe (es sei denn, man hat dies unterbunden) in der Ausgaberegion, darauf dann wieder eine Eingabezeile, usw. Dazwischen lassen sich nach Belieben Kommentare (Textbereiche) und Graphiken (Graphikbereiche) einfügen. Alle Bereiche bis auf den Eingabebereich werden bei der Ausführung/Berechnung des Arbeitsblattes von Maple übergangen.
Die Schriftzeichen (Fonts) der Eingaberegion, Textregion und Ausgaberegion lassen sich den Präferenzen des Anwenders gemäß ändern (s.u.).
Bei der MS Windows-Version von Maple V stehen mehrere Tastaturkommandos zur Verfügung, die die Gestaltung des Arbeitsblattes steuern:
Jede Kommandozeile muß entweder mit einem Semikolon (semicolon) oder einem Doppelpunkt (colon) jeweils gefolgt von Return oder Enter abgeschlossen werden. Dabei bewirkt das Semikolon die Berechnung und die Anzeige des Ergebnisses, der Doppelpunkt nur die Berechnung, aber nicht die Anzeige des Resultates. Der Abschnitt 'Ergebnisspeicher' beinhaltet eine kleine Demonstration.
Menü FILE
Mit dem Eintrag New kreieren Sie ein neues Arbeitsblatt. Seit Release 4 können Sie während einer Maple-Sitzung ein oder mehrere Arbeitsblätter geöffnet halten.
Open öffnet bzw. lädt ein Arbeitsblatt, welches entweder im MWS-Format von Release 4 und 5, dem Release 3-MS- oder einfachen ASCII-Format vorliegen kann. MWS- und MS-Dateien beinhalten sowohl die Ein- als auch Maple-Ausgaben, Formatierungen sowie evtl. eingebettete Graphiken, in ASCII-Dateien sind nur die Benutzereingaben gespeichert.
Save speichert den aktuellen Inhalt des Arbeitsblattes in eine bereits bestehende Datei; mit Save As speichern Sie ein neues Arbeitsblatt unter einem beliebigen Dateinamen ab. Das Zielverzeichnis können Sie dabei ebenfalls wählen. Anders als bei Save erscheint eine Warnmeldung, wenn eine bereits vorhandene Datei überschrieben werden soll. Maple speichert zwar alle Ein- und Ausgaben, Text sowie Graphiken in die MS-Datei, nicht aber die errechneten Werte bzw. den Zustand der Arbeitssitzung.
Der Menüpunkt Export As ermöglicht es, Arbeitsblätter als ASCII-, LaTeX- oder HTML-Dateien abzuspeichern.
Close schließt das aktuelle Arbeitsblatt.
Mit Save Settings werden gewisse das Arbeitsblatt betreffende Formatierungseinstellungen gespeichert, wie z.B. die Anzeige von Bereichsklammern oder der Statusleiste. Diese Einstellungen gelten dann für alle folgenden Arbeitssitzungen. Auto save Settings speichert die die Benutzereinstellungen fortwährend ab.
Print druckt das Arbeitsblatt auf Papier, Print Preview gibt eine Vorschau des Ausdruckes am Bildschirm aus, mit Printer Setup lassen sich druckerspezifische Einstellungen treffen.
Exit schließlich beendet Maple.
Menü EDIT
Benutzereingaben bzw. Formatierungen lassen sich mit Undo über mehrere Ebenen wieder aufheben. Zuvor markierte Textpassagen können in die Zwischenablage kopiert (Copy), aus der Zwischenablage in das Arbeitsblatt (oder auch in ganz andere Programme) eingefügt (Paste) oder gelöscht (Delete) werden. Mit Cut wird Text ausgeschnitten und in die Zwischenablage kopiert.
Delete Paragraph löscht die aktuelle Region aus dem Arbeitsblatt, Select All markiert alle Bereiche sowie deren Inhalte.
Split or Join erlauben es, eine Region in zwei Bereiche zu unterteilen bzw. wieder zusammenzufügen. Execute führt die in den zuvor markierten (Selected) Eingaberegionen enthaltenen Anweisungen aus oder berechnet alle Eingaben vom Anfang des Arbeitsblattes bis zu dessen Ende (Worksheet). Remove Output entfernt entweder nur markierte (Selection) oder alle (Worksheet) Maple-Ergebnisse.
Menü VIEW
Mit diesem Menüpunkt werden Festlegungen für die Darstellung von Inhalten getroffen oder bestimmte Paletten eingeblendet.
Die diversen Leisten können durch Anklicken der folgenden Menüeinträge entweder ein- oder ausgeblendet werden. Eingeblendete Leisten sind durch ein Häkchen markiert.
Release 5 bietet drei unterschiedliche Paletten an, mit denen griechische Buchstaben (Symbol Palette), vorformatierte mathematische Ausdrücke (Expression Palette) , z.B. Integrale, Summen, Grenzwerte, etc., oder auch Matrizen (Matrix Palette) in das Arbeitsblatt eingefügt werden können.
Mit Zoom Factor läßt sich die Bildschirmdarstellung entweder vergrößern (> 100 %) oder verkleinern (< 100 %). Mit Bookmarks werden HTML-ähnliche Sprungadressen (Labels) definiert, zu denen aus anderen Arbeitsblattbereichen oder anderen MWS-Dateien gesprungen werden kann.
Show Invisible Characters zeigt, wenn aktiviert, im Arbeitsblatt befindliche Steuerzeichen wie RETURN, Tabulatoren, o.ä. an. Show Section Ranges sowie Show Group Ranges blenden die umschließenden Klammern von Sektionen bzw. Bereichsklammern entweder ein oder aus. Sektionen sind spezielle Regionen, welche Ein- und Ausgaben sowie Texte und Graphiken enthalten können, die jedoch durch den Benutzer durch Mausklick ein- oder ausgeklappt werden können. Expand All Sections sowie Collapse All Sections stellen alle Sektionsinhalte dar oder aber blenden sie aus.
Menü INSERT
Statt die F5-Taste zu betätigen, können an der aktuellen Cursorposition über die Menüpunkte Text Input bzw. Maple Input entweder Text oder Mapleanweisungen eingegeben werden. Befindet sich der Cursor in einer Textregion und drücken Sie dort die F5-Funktionstaste bzw. wählen den Menüpunkt Maple Input, so können Sie an dieser Stelle Ausdrücke in mathematischer Schriftsetzung einfügen.
_ber den Punkt Execution Group können weitere Eingaberegionen entweder vor (Before Cursor) oder hinter (After Cursor) der aktuellen Position des Cursors dem Arbeitsblatt hinzugefügt werden.
Menü FORMAT
Diverse Formatierungseinstellungen z.B. für Maple- oder -ausgaben, Fließtext oder _berschriften lassen sich über den Menüpunkt Styles treffen.
Befindet sich der Cursor in einer Textregion, so können Sie markierte Passagen entweder kursiv (Italic), fett (bold) oder unterstrichen (Underline) darstellen.
Text und Mapleeingaben lassen sich entweder links- oder rechtsbündig (Left bzw. Right Justify) oder zentriert (Center) ausrichten.
Menü OPTIONS
Replace Output ersetzt alte durch neu berechnete Maple-Ergebnisse, andernfalls werden die neuen Ergebnisse unter die alten gesetzt. Ist Insert Mode aktiviert, so wird nach der Betätigung der Return-Taste automatisch eine Eingaberegion bzw. ein Prompt unter die zuletzt berechnete Maple-Ausgabe in das Arbeitsblatt eingefügt.
Menü HELP
Maple V enthält eine exzellente Online-Hilfe, die ausführliche Informationen zu jedem Befehl bzw. Thema anbietet. Mit Topic Search rufen Sie die Hilfeseite(n) zu einem Maple-Kommando auf, Full Text Search sucht in allen Hilfeseiten nach der eingegeben Zeichenfolge. History gibt eine Liste aller in der aktuellen Sitzung aufgerufenen Hilfethemen aus.
Die Grundrechenarten Addition (+), Subtraktion (-), Multiplikation (*), Division (/) sowie Potenzierung (^):
> 4+6;
> 4-10;
> 8*9;
> 2.1/6;
> 2^3;
Das Hütchen (Caret) ^ erzeugen Sie auf einem PC, indem Sie die ^-Taste (links neben der Taste '1') betätigen, sie danach loslassen und dann eine weitere Taste (hier 3) drücken; danach erst erfolgt die Anzeige des ^-Symboles.
Weitere einfache Operationen:
> x^a;
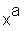
> 3*5-5.5*9+6;
> sqrt(2);
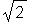
> 2^(1/3);
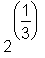
sqrt ermittelt die Quadratwurzel eines Ausdruckes, alle anderen Wurzeln können entweder in ihrer Potenzschreibweise eingegeben oder mit dem Befehl surd berechnet werden.
Die Namen einfacher mathematischer Funktionen gleichen im Ungefähren denen eines normalen wissenschaftlichen Taschenrechners. Argumente (arguments) von Funktionen und Befehlen werden grundsätzlich in runde Klammern gesetzt:
> sin(Pi);
> exp(1);
Eine Besonderheit besteht bei ganzzahligen Divisionen: Sie erhalten hier keinen Fließkommawert als Ergebnis, sondern einen (unausgewerteten) Bruch (fraction), sprich einen rationalen Ausdruck. Maple verwaltet diesen intern - anders als Fließkommaausdrücke - mit absoluter Genauigkeit.
> 5/8;
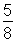
Wünschen Sie aber die Dezimaldarstellung numerischer Werte, so reicht es, hinter einer Zahl im Bruch einen Punkt zu setzen, oder den Bruch dem Befehl evalf zu übergeben.
> 5./8;
> evalf(5/8);
Die Genauigkeit von Fließkommaberechnungen (floating point notation), d.h. die Anzahl der verwendeten Fließkommastellen (genauer: die der Mantisse), läßt sich durch die Systemvariable Digits ändern, der Vorgabewert ist 10. Eine Erhöhung des Wertes führt bei komplexen Berechnungen zu einer längeren Rechenzeit.
> Digits := 20;
> evalf(1/3);
Unabhängig davon kann die Genauigkeit einer einzelnen Fließkommadarstellung als Option durch evalf(ausdruck, genauigkeit) vorgeben werden:
> evalf(Pi, 50);
Hier wird die Zahl Pi mit 50 Stellen angezeigt.
Hinweis: In älteren Versionen von Maple V wird statt des Prozentzeichens das Anführungszeichen (double quote / ditto) verwendet. Das Ditto wird in Release 5 jedoch zur Begrenzung von Zeichenketten genutzt.
> restart: > sin(2): > cos(2);
> tan(2);
> %%%;
Das zweifache Prozentzeichen bezieht sich auf die Anzeige von tan(2):
> %%;
Das jetzt folgende einfache Prozentzeichen greift auf das Ergebnis zurück, den die vorherige Zeile geliefert hat:
> %;
Ein neu berechneter bzw. angezeigter Wert bewirkt immer die Neubelegung des Ergebnisspeichers, daher führt folgende Reihenfolge nicht zum Ziel:
> sqrt(1);
> sqrt(2);
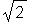
> sqrt(3);
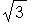
> %;
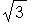
> %%;
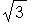
> %%%;
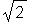
> sin(Pi);
> Sin(Pi);
Obwohl Maple V Sin nicht kennt, erfolgt kein Fehlermeldung.
Eingaben können Sie auch über mehrere Zeilen verteilen, wenn diese durch SHIFT-RETURN voneinander getrennt wurden:
> 3*9 > ;
> 3 > * > 9 > ;
> 3* > 9;
Die Wertzuweisung (assignment) von Ausdrücken an Variablen erfolgt wie bei den Programmiersprachen der ALGOL-Familie (u.a. MODULA-2 oder PASCAL) mit ':=', also einem Doppelpunkt gefolgt von einem Gleichheitszeichen. Es können hierbei nicht nur Zahlenwerte, Variablen und Terme sondern auch Gleichungen benannt werden. Für die Namen der Ausdrücke gelten folgende Regeln:
Erlaubte Variablennamen sind u.a.:
Den Wert einer Variablen erfahren Sie durch Eingabe ihres Namens mit abschließendem Semikolon.
Das einfache Gleichheitszeichen '=' dient nur dem Vergleich von Ausdrücken, es kann nicht zur Wertdeklaration herangezogen werden, wie in der Schulmathematik oder beispielsweise BASIC oder FORTRAN üblich.
> u := 50;
> u;
> y := 4*x-3;
Der Wert von y (also 4x - 3) wird jetzt automatisch in die Variable y der folgenden Zeile eingesetzt.
> y^2+5*x+3;
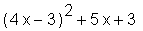
Nun folgt eine Zuweisung einer Gleichung an eine Variable; die Gleichung enthält wieder die bereits bestimmte Variable y. Setzen Sie eine Variable in Apostrophe, so wird sie in der betreffenden Zeile unausgewertet angezeigt. Dennoch bleibt im Gegensatz zu der Löschung von Variablen durch var:='var' (s.u.) der Wert von y erhalten, siehe übernächste Zeile.
> gleichung := 'y'*67=x+6;
> gleichung;
Ein Zuweisungsversuch an einen Maple-Befehl schlägt generell fehl:
> solve := 9; Error, attempting to assign to `solve` which is protectedDie Fehlermeldung weist darauf hin, daß der Name 'solve' geschützt ist.
Ein unerlaubter Bezeichner:
> 3n := 90; syntax error: 3n:=90; ^Der Versuch der Zuweisung mit '=' scheint zwar zuerst zu funktionieren:
> B9=10;
aber eine Wertbelegung erfolgt nicht:
> B9;
Groß- und Kleinschreibung bei Variablen:
> Variable := 1;
> variable := 2;
> Variable;
> variable;
Siehe auch assign im Abschnitt 'Gleichungen' in Kapitel 2.
Die Funktionszuweisung unterscheidet sich von der von der Schule gewohnten Art, sie erfolgt mittels der sog. 'Pfeilzuweisung' (arrow notation). Es gelten dieselben Namensregeln wie bei Variablen.
> f := x -> 1/4*x^4-4*x;
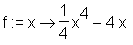
> f(7.);
Das Pfeilsymbol ->besteht aus dem Minus- und dem Größerzeichen.
Obschon in dieser Abhandlung nicht die Programmierung Maples erläutert werden soll, möchte ich die for-Schleife kurz erklären, mit deren Hilfe eine Wertetabelle erstellt werden kann. Die Zeilen trennen Sie durch die Tasten SHIFT+RETURN voneinander (gleichzeitig drücken), hinter der letzten Zeile aber betätigen Sie nur die RETURN-Taste.
> for xneu from -2 to 2 by 0.5 do > lprint(xneu, evalf(f(xneu))) > od; -2 12. -1.5 7.265625000 -1.0 4.250000000 -.5 2.015625000 0 0 .5 -1.984375000 1.0 -3.750000000 1.5 -4.734375000 2.0 -4.000000000Die for-Schleife erlaubt die mehrmalige Abarbeitung bestimmter Anweisungen, welche sich im Rumpf zwischen do und od befinden. Dabei steht die Anzahl der Wiederholungen im voraus fest. In diesem Beispiel werden alle Werte von (from) -2 bis (to) +2 durchlaufen, mit einer Schrittweite (by) von 0.25, und der 'Laufvariablen' xneu zugeordnet. Soll die Schrittweite Eins betragen, so kann sie weggelassen werden, der Passus 'by 1' kann also entfallen. lprint bewirkt die Ausgabe der Werte von xneu und f(xneu). (Sie können auch den Befehl print benutzen.) Sollen mehrere Befehle im Rumpf abgearbeitet werden, so müssen sie durch Semikolon voneinander getrennt werden. Hinter do allerdings darf sich kein Semikolon befinden.
Eine Funktionsdefinition wie
> t(x) := x^2;
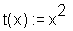
ist zwar möglich, doch führt dies nicht weit:
> evalf(t(7));
Funktionsdefinition mit mehreren Variablen:
> g := (x, y, z) -> sin(x) + cos(y) + tan(z): > g(Pi, a, Pi/4);
Bei zwei oder mehr Argumenten müssen diese hinter dem Zuweisungsoperator := in Klammern gesetzt werden.
Die Namen von Variablen und Funktionen sollten sich nicht gleichen, da es hierbei zu Kollisionen kommt. Im folgenden wird eine Variable r und eine Funktion r(x) definiert, nach der Funktionszuweisung ist der Wert der Variable gelöscht:
> r := 10;
> r := x -> x^2;
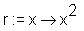
> r;
> r(x);
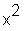
Einmal wird r der Wert 10 und dann eine Funktionsvorschrift x->x^2 zugewiesen.
Alle während der Sitzung (session) gespeicherten Variablen, Funktionen und aufgerufenen Pakete können Sie durch restart wieder löschen (sog. 'Reset').
> i := 10;
> p := x -> x^2: > i;
> p(x);
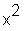
> restart: > i;
> p(x);
Löschen (unassignment) können Sie einzelne Variablen durch eine Zuweisung der Form
(Hierbei befindet sich die Apostrophtaste ' rechts neben dem 'ä'.)
> z := 10;
> z;
> z := 'z';
> z;
Löschen von Funktionszuweisungen:
> restart: > f := x -> x^2: > f(x);
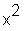
> f := 'f';
> f(x);
Maple enthält eine umfangreiche und gut dokumentierte Hilfefunktion zu den einzelnen Kommandos, welche Sie mit ?kommando (ohne abschließendes Semikolon) aufrufen können. ??kommando liefert die Syntax des entsprechenden Kommandos und ???kommando bzw. example(kommando); Beispiele zu diesem.
> ?solve > ??solve > ???solveinfo(kommando); gibt die Beschreibung des Befehles wider:
> info(solve);related(kommando); listet verwandte Befehle auf:
> related(solve);
> convert(x^2, binary); Error, (in convert/binary) invalid argument for convertHier sollte das Polynom in die Binärdarstellung umgeformt werden, welches unsinnig ist.
Eine andere Fehlerquelle sind Syntaxfehler:
> 4+*4; syntax error: 4+*4; ^Ein Operator wurde oben zuviel angegeben. Der Pfeil zeigt die Stelle, die den Fehler hervorrief, an.
> 3*4; syntax error: 3*4; ^Hier wurde '3*4' ohne Semikolon oder Doppelpunkt eingegeben, mit Enter zur nächsten Zeile gesprungen, dann der Cursor eine Zeile wieder nach oben bewegt und hinter '3*4' ein Semikolon gesetzt und nachfolgend Enter gedrückt.
Oft können auch Parameter vergessen werden:
> diff(x^2); Error, wrong number (or type) of parameters in function diff > diff(x^2, x);
In der Mathematik ist ein Ausdruck wie 'mx', welches 'm multipliziert mit der Unbestimmten x' bedeutet, üblich. Dies führt bei Maple allerdings zu einer Fehlermeldung:
> 2x; syntax error: 2x; ^ > 2*x;
Es muß grundsätzlich das Multiplikationszeichen * angegeben werden. Gleichwohl erfolgt die Anzeige ohne das Multiplikationszeichen.
Zu den häufigsten Fehlerquellen gehören falsch gesetzte oder vergessene Klammern.
> limit(1+1/n^n, n=infinity);
> limit((1+1/n)^n, n=infinity);
Fehlende Klammern werden mit einem Syntaxfehler quittiert:
> sum(1+2/n)^n, n=infinity);
syntax error:
sum(1+2/n)^n, n=infinity);
^
Tippfehler bei Kommandos ergeben keine Fehlermeldung, sondern es wird die Eingabe unberechnet wieder ausgegeben.
> sum((1+2/n)^n, n=infinty);
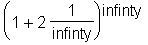
Her fehlt bei infinity das letzte 'i'.
MAPLE EINFÜHRUNG - MPLINTRO 04.00a vom 14. Dezember 1998
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/m1.htm