

This is a variation of the procedure Alex' Error by plotting the trajectory a point traverses through iteration of the formula
Files for download:
> restart: > orbits := proc(x, y, iter) > local c, z, pts; > pts := NULL; > c := evalf(x+y*I); > z := c; > to iter do > if abs(z) < 1e10 then > pts := pts, [Re(z), Im(z)] > fi; > z := z^2+c > od; > [pts] > end: > plot(orbits(-0.14222874119878, -0.64732701703906, 500), style=point, > symbol=POINT, axes=framed, scaling=constrained);

> plot(orbits(-0.50977517291904, -0.60039090737700, 500), style=point, > symbol=POINT, axes=framed, scaling=constrained);
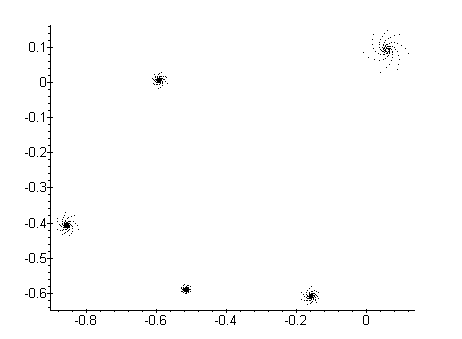
> plot(orbits(-0.50977517291904, -0.60039090737700, 300), style=line, > axes=framed, scaling=constrained);

> # orbits1.gif 'Spiral' > plot(orbits(-0.61143695190549, -0.36571035906672, 500), style=point, > symbol=POINT, axes=framed, scaling=constrained); > # orbits3.gif 'Vortex' > plot(orbits(-0.34555229917169, -0.60430224984884, 300), style=point, > symbol=POINT, axes=framed, scaling=constrained); > # orbits4.gif > plot(orbits(+0.24877810105681, +0.58083451911807, 115), style=line, > axes=framed, scaling=constrained); > # orbits5.gif 'Radiation' > plot(orbits(-0.33382209390402, -0.60821359232068, 500), style=point, > symbol=POINT, axes=framed, scaling=constrained); > # orbits6.gif > plot(orbits(-0.25953079387546, -0.62385896220803, 500), style=point, > symbol=POINT, axes=framed, scaling=constrained); > plot(orbits(-0.14222874119878, -0.64732701703906, 300), style=line, > axes=framed, scaling=constrained);
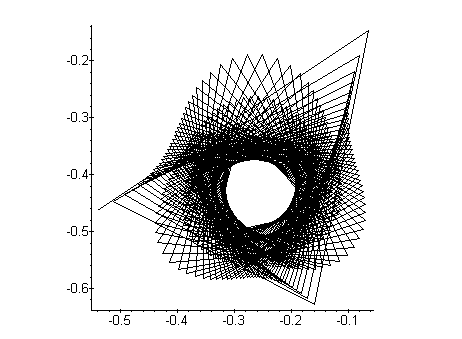
Points at the vicinity of the fractal coastline of the Mandelbrot set result in the most interesting orbits.
Another version of the above procedure computes the orbits of a point in three dimensions, where the third dimension (height) depicts the repective of iteration.
> restart: > orbits3d := proc(x, y, iter) > local c, z, pts, i; > pts := NULL; > c := evalf(x+y*I); > z := c; > for i to iter do > if abs(z) < 1e10 then # avoid overflow > pts := pts, [Re(z), Im(z), i] > fi; > z := z^2+c > od; > [pts] > end: > plots[spacecurve](orbits3d(0.2, 0.5, 50), > x=-2 .. 2, y=-2 .. 2, style=line, axes=framed, orientation=[45, 45]);

MAPLE V FRACTALS MandelbrotOrbits #1.1 current as of May 22, 1999
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mfrorbit.htm