Category: Attractor Fractal

This is a visualization of Newton's method to calculate the complex solution of zⁿ-1 = 0 by using the iteration formula

with fn(z) := zⁿ - 1, and n > 2 the polynomial degree of fn (also real values for n are allowed).

> solve(z^3-1=0, z);

The graph shows the starting points from which the method does or does not converge to one of the above roots. The documentation of FRACTINT explains the result: "The coloring of the plot shows the "basins of attraction" for each root of the polynomial -- i.e., an initial guess within any area of a given color would lead you to one of the roots. As you can see, things get [fractal] along certain radial lines or "spokes," those being the lines between actual roots." The fractal properties of Netwon's method to calculate complex roots were first discovered by John Hubbard of Orsay, France.

> restart: 

> newton := proc(x, y)
>    local z, m;
>    z := evalf(x+y*I);
>    for m from 0 to 50 while abs(z^3-1) >= 0.001 do
>       z := z - (z^3-1)/(3*z^2)
>    od;
>    m
> end:

> plot3d(0, -2 .. 2, -1.5 .. 1.5, orientation=[-90,0], 
>    grid=[250, 250], style=patchnogrid, scaling=constrained, 
>    color=newton);

The following statements have been taken from the book Maple V Release 4 written by Michael Kofler and published by Addison-Wesley. It uses the complexplot3d function which is new with Release 4. However, with large values for 'grid', this command uses a very large amount of memory so Windows systems missing the proper resources are likely to crash with complexplot3d. The following images are the views of the Maple plot from different orientations. The computation consumed around 11 Mbytes of memory.

> p := (z-1)*(z^2+z+5/4);

> f := unapply(z-p/(diff(p,z)-0.5*I), z);

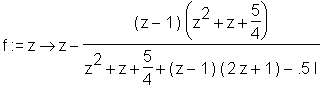
> complexplot3d(f@@4, -4-4*I .. 4+4*I, view=-1 .. 2, 
>    style=patchnogrid, orientation=[-143, 65], 
>    grid=[150, 150]);

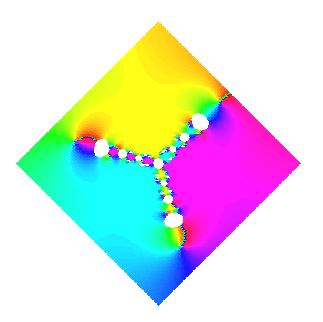
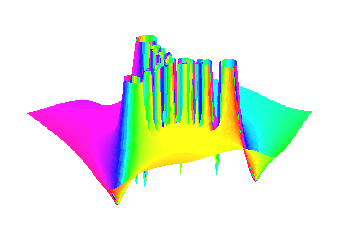
MAPLE V FRACTALS NEWTON #1.01 current as of May 23, 1999
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mfrnewt.htm