

Diese Routine stammt von John Oprea und vermeidet auf intelligente Weise hohe Berechnungszeiten, indem das Fraktal mittels plot3d und dessen Farboption color dargestellt wird. Dadurch gelingt es auch, die Mandelbrot-Menge in der Ebene - und nicht im Raum - darzustellen. Würde man versuchen, mittels plot ein Fraktal anzuzeigen, so wären alle Punkte der Menge in einer Liste abzuspeichern, da Punkte in Maple V nicht direkt gesetzt werden können, wie beispielsweise in vielen Programmiersprachen mit einem `PutPixel`-Befehl möglich. Die Nutzung einer Liste aber ist sehr speicheraufwendig und kann ferner zum Absturz Maples (bzw. zum Abbrechen der Berechnung) führen.
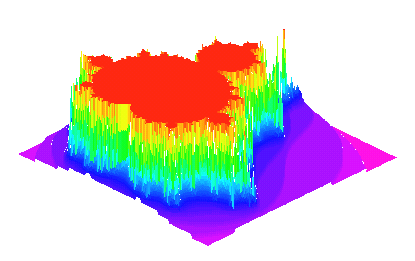
# The Mandelbrot set # # 2D display coding by John Oprea, oprea@math.csuohio.edu > restart: with(plots): > mandelbrot := proc(x, y) > local c, z, m; > c := evalf(x+y*I); > z := c; > for m to 30 while abs(z) < 2 do > z := z^2+c > od; > m > end: > plot3d(0, -2 .. 0.7, -1.2 .. 1.2, orientation=[-90,0], > grid=[250, 250], style=patchnogrid, > scaling=constrained, color=mandelbrot);

(Die Bezeichnungen entstammen dem Buch Fractals for Windows von Tim Wegner, Bert Typler, Mark Peterson, und Pieter Branderhorst, The Waite Group.)
> plot3d(0, --0.83561 .. -0.78523, 0.15559 .. 0.19343, orientation=[-90,0], > grid=[250, 250], style=patchnogrid, scaling=constrained, > color=mandelbrot);

eingesetzt, wobei anfänglich c = z0 = 0 gesetzt wird. Die Berechnung nach obiger Formel wird nun für jedes c beliebig oft durchgeführt, es entsteht für jedes c eine Zahlenfolge z0, z1, z2, usw. Nach jeder Iteration wird geprüft, ob sich zn+1 innerhalb eines bestimmten Radius um den Ursprung befindet, hier setzen wir den Radius gleich 2.
> restart: > MandelbrotOrbit := proc(x, y, iter) > local c, z, pts; > pts := NULL; > c := evalf(x+y*I); > z := 0; > to iter do > pts := pts, [Re(z), Im(z)]; > z := z^2+c > od; > [pts] > end:Betrachten wir die Zahlenfolge für c = 0 + i für 10 Iterationen:
> MandelbrotOrbit(0, 1, 10);
[[0, 0], [0, 1.], [-1., 1.], [0, -1.], [-1., 1.], [0, -1.], [-1., 1.],
[0, -1.], [-1., 1.], [0, -1.]]
Diese Zahlenfolge verhält sich periodisch und wechselt bei n > 1 zwischen -1 + i und -i. c = i ist also Teil der Mandelbrot-Menge.
c = 0.5 + 0.3i:
> MandelbrotOrbit(0.5, 0.3, 10); [[0, 0], [.5, .3], [.66, .60], [.5756, 1.0920], [-.36114864, 1.55711040], [-1.794164458, -.824696607], [3.038901609, 3.259282682], [-.888000612, 20.10927877], [-403.0945476, -35.41410371], [161231.5556, 28550.76423]]Mit der Zahl c = 3.038901609 + 3.259282682i
> abs(3.038901609 + 3.259282682*I);
4.456214379
verläßt der Orbit den Radius 2. c = 0.5 + 0.3i ist also nicht Teil der Mandelbrot-Menge. Folgende Graphik macht den Sachverhalt anschaulich:
> with(plots):
> xyranges := x=-2.5 .. 2.5, y=-2.5 .. 2.5:
> plotoptions := style=line, symbol=POINT, scaling=constrained:
> p1 := plot(MandelbrotOrbit(0.5, 0.3, 10), xyranges,
> plotoptions, color=navy):
> p2 := plot(MandelbrotOrbit(0.2, 0.5, 100), xyranges,
> plotoptions, color=black):
> p3 := plot(MandelbrotOrbit(0, 1, 100), xyranges,
> plotoptions, color=maroon):
> radius := implicitplot(x^2+y^2=4, xyranges):
> display({p1, p2, p3, radius}, axes=box);
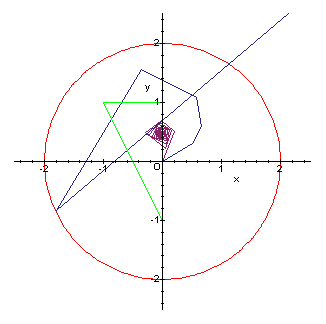
Da nicht eine unendliche Anzahl von Iterationen pro Punkt durchgeführt werden kann, um zu bestimmen, ob dieser Punkt zur Mandelbrot-Menge gehört oder nicht, begrenzt man die Anzahl der Iterationen auf einen endlichen Wert n (sog. Abbruchwert). Es ist also nicht sicher, ob ein Punkt, der nach n Iterationen innerhalb des Radius 2 blieb, ihn nach n+1 Iterationen nicht doch noch überschreitet.
In der Prozedur mandelbrot fehlt die anfängliche Zuweisung z = 0, dieses wird übergangen und statt dessen direkt z = c gesetzt.
Unter MandelbrotFast wird eine Prozedur zur Beschleunigung der Berechnung vorgestellt, MandelbrotOrbits zeigt weitere Bilder der Orbits.
Verschiedene Teile der Mandelbrot-Menge können durch Ändern des zweiten und dritten Argumentes der plot3d-Anweisung erforscht werden.
style=patchnogrid zeichnet die Fläche mit schattierten, rechteckigen Feldern, aber ohne ein Gitternetz, dieses ist die beste Stiloption für den Graphen.
> restart: > mandelbrot := proc(x, y) > local z, m; > z := evalf(x+y*I); > for m from 0 to 30 while abs(z) < 2 do > z := z^2+(x+y*I) > od; > m > end: > plot3d(mandelbrot, -2 .. 0.7, -1.2 .. 1.2, grid=[150, 150]);
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mfrmandd.htm