

Category: Escape-time Fractal
Julia sets are related to the Mandelbrot set in that the formula generating both is the same. The only difference is that for the Mandelbrot set the variable c is assigned the coordinates of the respective point [x, y] being iterated, so c changes for each point in the plane. In contrast, with Julia sets the variable c always remains the same for all the points in the plane:
| Name | Iteration formula | Initialization of z | Initialization of c |
| Mandelbrot set | zn+1 := zn + c | z0 := x + I*y | c = z0 (variable) |
| Julia sets | zn+1 := zn + c | z0 := x + I*y | c = a + I*b (fixed) |
Thus, the Mandelbrot set can be seen as some sort of `catalogue` of Julia sets.
> restart; with(plots): # Julia sets # # written by John Oprea, oprea@math.csuohio.edu > julia := proc(c,x, y) > local z, m; > z := evalf(x+y*I); > for m from 0 to 30 while abs(z) < 3 do > z := z^2 + c > od; > m > end: > J := proc(d) > global phonyvar; > phonyvar := d; > (x, y) -> julia(phonyvar, x, y) > end: > plot3d(0, -2 .. 2, -1.3 ..1.3, style=patchnogrid, > orientation=[-90,0], grid=[250, 250], > scaling=constrained, color=J(-1.25));Users of the Student Edition of both Release 3 and 4 have to decrease the value of the grid option to [70, 70] because of the limitation of the array size to 5120 elements.
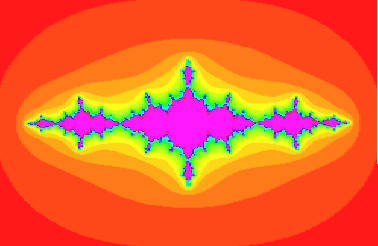

MAPLE V FRACTALS JULIA #1.1 current as of May 23, 1999
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mfrjulia.htm