|
Kapitel Fünf: Lineare Algebra, Analytische Geometrie und Kombinatorik |
 |
|
|
|
Kapitel 4
|
|
Kapitel Fünf: Lineare Algebra, Analytische Geometrie und Kombinatorik |
 |
|
|
|
Kapitel 4
|
Beginnen wir zunächst mit der Definition von Vektoren. Obschon sie mit dem Maple-Standardbefehl array definiert werden können, existiert im Paket linalg die Anweisung vector, welche benutzerfreundlicher ist. Ein Vektor besteht aus seinen Komponenten a1 .. an. Seine Dimension ist beliebig: es lassen sich nicht nur Vektoren der Ebene, sondern auch des Raumes und höherer Dimensionen deklarieren, entsprechen aber im mathematischen Sinne Spaltenvektoren.
Es folgt eine Vorstellung der verschiedenen in Maple vorhandenen Operationen anhand dreidimensionaler Vektoren.
> restart: > with(linalg): Warning: new definition for norm Warning: new definition for trace > vec1 := vector([a1, b1, c1]);
> vec2 := vector([a2, b2, c2]);
Die Addition zweier Vektoren geschieht mit matadd (in R3 benutzen Sie hierfür bitte die Funktion linalg/add):
> matadd(vec1, vec2);
Die Subtraktion zweier Vektoren erfolgt ebenfalls mit matadd (R3: linalg/add), aber mit negativem Vorzeichen bei einem der Vektoren:
> matadd(vec1, -vec2);
Hinweis: Vektoraddition und - subtraktion können auch mit dem Maple-Standardbefehl evalm durchgeführt werden.
> evalm(vec1 + vec2); > evalm(vec1 - vec2);S-Multiplikation (scalar multiplication):
> scalarmul(vec1, s);
Vektor- oder Kreuzprodukt (cross product):
> crossprod(vec1, vec2);
Skalarprodukt (dot product) zweier Vektoren: a*b=|a|*|b|*cos(alpha):
> dotprod(vec1, vec2);
Ein Beispiel mit konkreten Vektoren; v1 und v2 sind zueinander orthogonal, wenn das Skalarprodukt 0 ist.
> v1 := vector([-3, 1, 2]);
> v2 := vector([2, -4, 5]);
> dotprod(v1, v2);
> matadd(v1, v2);
> scalarmul(v1, 2);
> crossprod(v1, v2);
Die Länge (2-Norm oder Euklidische Norm) eines Vektors wird mit norm(vektor, 2) bestimmt:
> norm(v1, 2);
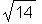
Winkel zweier Vektoren mit angle:
> angle(v1, v2);
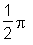
Die Radianten werden in Grad umgerechnet, v1 und v2 stehen aufeinander senkrecht:
> %*180/Pi;
normalize normiert einen Vektor auf die Länge 1:
> normalize(v1);
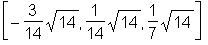
Matrizen können mit dem Befehl matrix aus dem Paket 'linalg' auf zweierlei Weise definiert werden: Entweder man übergibt dem Befehl direkt eine verschachtelte Liste, also eine Liste von Listen, welche jeweils aus den einzelnen Zeilenelementen bestehen, oder aber man gibt dem Befehl den genauen Typ der Matrix an (bestehend aus dem Eintrag m für die Anzahl der Zeilen und n für die Anzahl der Spalten -> (m, n)-Matrix) und eine Liste aller Matrixelemente, die Maple dann selbständig einordnet.
> restart: with(linalg): > A := matrix([[a, b], [c, d]]);
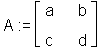
> A := matrix(2, 2, [a, b, c, d]);
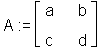
Benutzerfreundlicher ist der Befehl entermatrix, mit dem man interaktiv die einzelnen Matrixelemente in der Kommandozeile eingeben kann, die dann entsprechend zugewiesen werden. (In Release 5 muß die Eingabe der Werte jeweils mit einem Semikolon beendet werden.) Vorher ist es nötig, den Typ der Matrix Maple mitzuteilen. Eine (2, 2)-Matrix wird also wie folgt deklariert:
> A := matrix(2, 2);
> entermatrix(A); enter element 1,1 > a; enter element 1,2 > b; enter element 2,1 > c; enter element 2,2 > d;
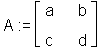
Hinweis: Das Paket math enthält die Funktion math/mat, mit der Sie Matrizen ohne Zuhilfenahme von Listen (Trennung der Zeilen) bzw. Kommata (Abtrennung der Koeffizienten) definieren können.
Fundamentale Matrixarithmetik:
Das Paket linalg stellt eine ganze Reihe von Befehlen für die Matrizenrechnung zur Verfügung. Um deren Anwendung demonstrieren zu können, definieren wir noch kurz eine Matrix B:
> B := matrix(2, 2, [e, f, g, h]);
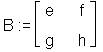
Die Befehle matadd (R3: add) und multiply aus linalg führen Matrixadditionen und -multiplikationen durch. Die Differenz zweier Matrizen erhalten Sie, indem die zweite Matrix im Argument des Kommandos matadd mit negativem Vorzeichen versehen wird (wie bei den Vektoren im vorherigen Abschnitt).
> Cadd := matadd(A, B);
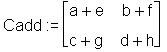
> Csub := matadd(A, -B);
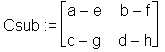
> Cmul := multiply(A, B);
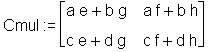
Determinanten quadratischer Matrizen werden mit det bestimmt:
> det(A);
Den Rang einer Matrix ermittelt rank:
> rank(A);
Die inverse Matrix:
> inverse(A);
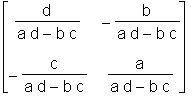
Um kurz den Effekt der Transposition zu verdeutlichen, wird die Matrix A neu definiert:
> A := matrix(2, 3, [a1, a2, a3, b1, b2, b3]): > evalm(A), transpose(A);
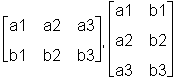
Eine Einheitsmatrix (also vom Typ n x n) wird durch die Anweisung
> Em := array(identity, 1 .. 3, 1 .. 3): evalm(Em);
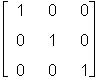
erzeugt.
Matrizenmanipulationen erlauben u.a. addrow, swaprow und mulrow. Darüber hinaus können Matrizen aus Vektoren oder anderen Matrizen mit augment gebildet werden:
> restart: with(linalg): > v1 := vector([a1, a2, a3]): > v2 := vector([b1, b2, b3]): > v3 := vector([c1, c2, c3]): > A1 := augment(v1, v2); # 2 Vektoren
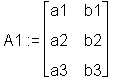
> A2 := augment(A1, v3); # Matrix und Vektor
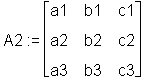
> augment(A1, A2); # 2 Matrizen

addrow multipliziert in der Matrix (erstes Argument) A2 die erste Zeile (zweites Argument) mit der Zahl 3 (viertes Argument) und addiert das Ergebnis zur zweiten Zeile (drittes Argument).
> addrow(A2, 1, 2, 3);
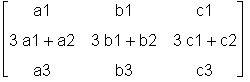
mulrow multipliziert in der Matrix A2 (erstes Argument) die erste Zeile (zweites Argument) mit dem Skalar 2 (drittes Argument).
> mulrow(A2, 1, 2);
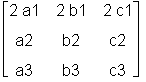
Zeilen werden mit swaprow vertauscht, hier in der Matrix A2 die erste mit der zweiten Zeile.
> swaprow(A2, 1, 2);
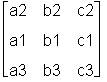
Lineare Gleichungssysteme in Matrizenform:
Die Lösung eines Systemes der Art A*x = c, wobei A die Koeffizientenmatrix, x der Lösungs- und c der Spaltenvektoren mit den Absolutgliedern sind, läßt sich mit linsolve berechnen. Werden unendlich viele Lösungen ermittelt, so werden in der Ausgabe Parameter verwendet, gibt es keine Lösung, so erfolgt keine Bildschirmausgabe.
> restart: with(linalg): > A := matrix([ > [1, -3, 1.5, -1], > [-2, 1, 3.5, 2], > [1, -2, 1.2, 2], > [3, 1, -1, -3]]): > c := vector([-10.4, -16.5, 0, -0.7]): > linsolve(A, c);
Man beachte die Rundungsfehler, die genauen Lösungen sind:
> A := matrix([ > [1, 1, -2], > [1, -1, -2], > [2, 3, -4]]): > c := vector([0, 0, 0]): > linsolve(A, c);
Lineare Gleichungssysteme können Sie in Matrizenform umwandeln. Gegeben sei folgendes System:
> restart: with(linalg):
> sys := {
> -2*x+2*y+7*z=0,
> x-y-3*z=1,
> 3*x+2*y+2*z=5}:
Mit genmatrix wird aus dem Gleichungssystem 'sys' mit den Unbekannten x, y und z
eine Matrix erstellt. Als dritter Parameter muß der Name 'flag' angegeben werden, damit die letzte Spalte nicht 'verschluckt' wird.
> temp := genmatrix(sys, [x, y, z], 'flag');
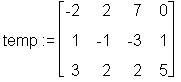
Mit gausselim wird das Gaußsche Eliminationsverfahren auf die erzeugte Matrix angewendet; das Ergebnis ist eine obere Dreiecksmatrix. backsub liefert die Lösung des reduzierten Systemes.
> gausselim(temp);
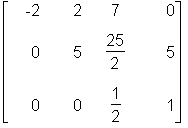
> backsub(%);
Aus einer Matrix lassen sich mit submatrix auch Untermatrixen erzeugen. Der erste Parameter ist die zu bearbeitende Matrix (hier 'temp'), der zweite und dritte die Zeilen- bzw. Spaltenbereiche, die kopiert werden sollen.
> A := submatrix(temp, 1 .. 3, 1 .. 3);
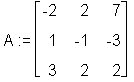
> c := submatrix(temp, 1 .. 3, 4 .. 4);
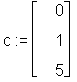
Die vierte Spalte können Sie aber einfacher mittels col (columns) kopieren.
> c := col(temp, 4);
> linsolve(A, c);
Ein dreidimensionales Histogramm:
> plots[matrixplot](temp, > heights=histogram, gap=0.15, axes=frame);
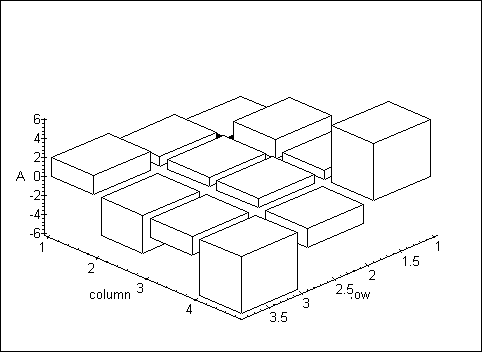
Zuletzt wird noch die Eigenwertberechnung einer Matrix vorgestellt. Auch hier leistet Maple nützliche Hilfe, indem mehrere Schritte zur Berechnung von Eigenwerten durch einen einzigen Befehl durchgeführt werden: eigenvals. Die Eigenwerte sind definiert durch:
mit A als Matrix, t als Parameter und Em als Einheitsmatrix, wobei nach Ermittlung der Determinanten das entstehende Polynom gleich Null gesetzt wird:
> restart: with(linalg): > A := matrix(3, 3, [0, -1, 0, -1, -1, 1, 0, 1, 0]): > Em := array(identity, 1 .. 3 ,1 .. 3): > solve(det(add(A, -t*Em))=0);
oder ganz einfach durch:
> eigenvals(A);
Die zweidimensionale Geometrie kann mit Paket geometry erforscht werden, dessen Syntax aber gewöhnungsbedürftig ist. (Die Pakete geometry und geom3d sind für Release 4 bzw. 5 vollkommen überarbeitet worden, die Syntax gleicht in vielen Fällen nicht mehr der der gleichnamigen Pakete in Release 3.)
> restart: > with(geometry):Zu Anfang der geometry-Sitzung sollten Sie zwei Umgebungsvariablen setzen, die Namen für die in den Objekten enthaltenen Unbekannten definieren:
> _ EnvHorizontalName := 'x': > _ EnvVerticalName := 'y':Definition zweier Punkte p1 und p2 mit point. Das erste Argument ist der Punkt, dem die Punktkoordinaten 2 und 3 als weitere Argumente zugewiesen werden.
> point(p1, 2, 3);
> point(p2, 0, 0);
Die in den geomtry-Objekten gespeicherten Werte ermittelt geometry/detail:
> detail(p1); name of the object: p1 form of the object: point2d coordinates of the point: [2, 3]Auf die Koordinaten in p1 greifen Sie mit geometry/coordinates zu:
> coordinates(p1);
Da die Variablen x und y intern durch das Paket geometry genutzt werden (sie sind global), sollte man ihre Werte nicht verändern.
Linien werden mit line definiert. Das erste Argument ist der Name der zu kreierenden Linie, gefolgt von der Angabe zweier Punkte in einer Liste.
> line(gerade, [p1, p2]);
> detail(gerade); name of the object: gerade form of the object: line2d equation of the line: 3*x-2*y = 0Die die Gerade darstellende Gleichung extrahiert geometry/Equation:
> geradengl := Equation(gerade);
Eine Gerade können sie auch durch eine Gleichung der Form a*x+b*y+c=0 definieren:
> line(g, 3*x-2*y=0);
Ein Kreis wird mit circle gebildet, dem der Name des Kreises sowie in einer Liste dessen Mittelpunkt p1 und Radius 2 übergeben werden:
> circle(kreis, [p1, 2]);
> detail(kreis); name of the object: kreis form of the object: circle2d name of the center: p1 coordinates of the center: [2, 3] radius of the circle: 2 equation of the circle: x^2+9+y^2-4*x-6*y = 0 > kreisgl := Equation(kreis);
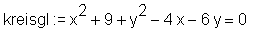
Der Graph des Kreises 'kreis' und der Geraden 'gerade':
> plots[implicitplot]({kreisgl, geradengl}, x=-2 .. 6,
> y=-1 .. 6, scaling=constrained);
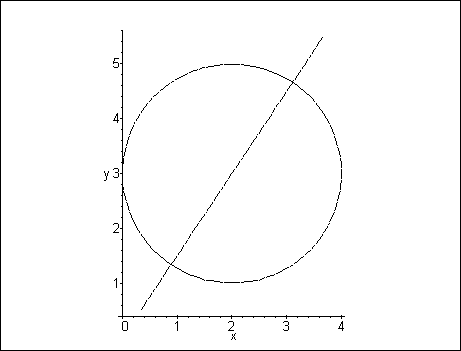
intersection ermittelt die Schnittpunkte (intersections) zweier Geraden oder aber eines Kreises mit einer Geraden. Als erstes Argument wird wieder der Name des zu erzeugenden Objektes genannt (hier schnitt), danach folgen der Kreis kreis sowie die Gerade gerade, deren Schnittpunkt(e) zu berechnen sind. Optional ist die Angabe der Bezeichnungen für die Schnittpunkte, welche in eine Liste einzutragen sind, hier [M, N].
> intersection('schnitt', kreis, gerade, [M, N]);
> detail(schnitt); name of the object: M form of the object: point2d coordinates of the point: [2+4/13*13^(1/2), 3+6/13*13^(1/2)] name of the object: N form of the object: point2d coordinates of the point: [2-4/13*13^(1/2), 3-6/13*13^(1/2)] > coordinates(M);
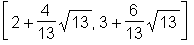
> coordinates(N);
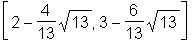
Die Kombination von map und coordinates ermittelt die Koordinaten mit einem Befehl.
> map(coordinates, [M, N]);
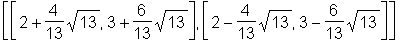
Für die Lagebeziehungen von geometrischen Objekten stehen einige Befehle zur Verfügung.
> restart: with(geometry): > line(g1, [point(a1, 0, 0), point(b1, -2, 3)]);
> line(g2, [point(a2, 0, 0), point(b2, 3, 2)]);
geometry/ArePerpendicular (R3: are_perpendicular) prüft, ob zwei Geraden aufeinander senkrecht stehen, also orthogonal sind.
> ArePerpendicular(g1, g2);
Parallelität zweier Geraden mit geometry/AreParallel (R3: are_parallel):
> AreParallel(g1, g2);
distance ermittelt die Entfernung eines Punktes von einem anderen Punkt oder einer Geraden. Syntax: distance(Punkt, Punkt oder Gerade).
> distance(a1, b1); # Entfernung zweier Punkte
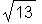
> distance(b2, g1); # Entfernung eines Punktes von einer Geraden
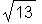
Zur Prüfung, ob ein Punkt (oder eine Liste von Punkten) auf einer Geraden liegt, nutzt man geometry/IsOnLine (R3: on_line).
> IsOnLine(b1, g1);
Das Paket geom3d beinhaltet Anweisungen zur dreidimensionalen Vektorrechnung. Die Syntax der Befehle gleicht zum größten Teil der des Paketes geometry.
Definition von Punkten im Raum:
> restart: with(geom3d): > point(a, [1, 1, 1]);
> point(b, [3, 4, 1]);
> point(c, [4, 3, -1]);
Geraden werden durch zwei Punkte gebildet:
> line(gerade1, [a, b]);
> detail(gerade1);
name of the object: gerade1
form of the object: line3d
assume that the name of the parameter
in the parametric equations is _t
assume that the name of the axis are _x, _y, and _z
equation of the line: [_x = 1+2*_t, _y = 1+3*_t, _z = 1]
oder durch Angabe eines Punktes und des Richtungsvektoren:
> line(gerade1, [a, [2, 3, 0]]);
Hinweis: der Vektor kann nicht mit vector aus dem Paket 'linalg' definiert werden.
Drei Punkte definieren eine Ebene:
> plane(ebene1, [a, b, c]);
> detail(ebene1); name of the object: ebene1 form of the object: plane3d assume that the name of the axis are _x, _y and _z equation of the plane: 7-6*_x+4*_y-5*_z = 0Ebenso erzeugen ein Punkt und ein Normalenvektor eine Ebene.
> plane(ebene2, [a, [3, 2, 1]]);
Eine Kugel bestehend aus dem Mittelpunkt c und einem Radius (oder aus vier Punkten):
> sphere(kugel, [c, 5]);
> detail(kugel); name of the object: kugel form of the object: sphere3d name of the center: c coordinates of the center: [4, 3, -1] radius of the sphere: 5 surface area of the sphere: 100*Pi volume of the sphere: 500/3*Pi assume that the name of the axis are _x, _y and _z equation of the sphere: _x^2+_y^2+_z^2+1-8*_x-6*_y+2*_z = 0Schnittgeraden, das Ergebnis wird im ersten Argument gespeichert.
> intersection(schnitt, ebene1, ebene2);
> Equation(schnitt);
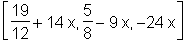
Für diesen Themenbereich existiert das Paket combinat.
choose ermittelt alle Kombinationen einer Liste von Elementen, der zweite optionale Parameter n berechnet nur n-elementige Kombinationen.
> restart: with(combinat): > s := [a, b, c]: > choose(s);
numbcomb gibt die Anzahl der Kombinationen einer Liste an.
> numbcomb(s);
> choose(s, 2);
Die Anzahl von Möglichkeiten, aus n Elementen m auszuwählen, beträgt bekanntlich 'binomial(n, k)'. Beispielsweise mit n=4 und k=3:
> binomial(4, 3);
> choose(4, 3);
Die Anzahl von Einträgen in eine Liste ermittelt nops, in diesem Falle die Anzahl der Unterlisten, welches mit 'binomial(4, 3)' identisch ist:
> nops(%);
Für Permutationen ist permute zuständig, wobei numbperm die Anzahl der Permutationen berechnet. Auch hier führt ein zweiter Parameter n wieder dazu, daß nur n-elementige Permutationen ausgegeben werden.
> permute(s);
> numbperm(s);
> permute(s, 2);
> numbperm(s, 2);
Das Cartesische Produkt wird auf eine etwas eigenwillige Weise ermittelt, da combinat/cartprod eine Tabelle zurückgibt, die eine Prozedur enthält, welche widerum mittels Aufruf durch eine while-Schleife alle Paare bestimmt. Solange (while) T[finished] nicht den Wert true annimmt, wird der nächste Wert ('nextvalue') berechnet (do). Siehe hierzu auch das Paket math, welches ein einfach zu bedienendes Interface math/cartprod für combinat/cartprod enthält.
> T := cartprod([[1,2], [a,b]]): > while not T[finished] do T[nextvalue]() od;
Die Stirlingsche Zahlen zweiter Art (Stirling numbers of the second kind) können Sie mit stirling2 finden, für den Fall S(n, k) mit n > k z.B.:
> stirling2(4, 2);
oder für n < k (immer gleich Null)
> stirling2(1, 2);
Die Bell-Zahlen bn:
> bell(4);
Für die Berechnung aller Partitionen einer natürlichen Zahl n steht partition bereit. Das Ergebnis ist eine 'Liste von Listen' (d.h eine Liste, in denen weitere Unterlisten enthalten sind). Die einzelne Elemente der jeweiligen Unterlisten ergeben als Summe die Zahl n. Optional und nicht dokumentiert ist ein zweiter Parameter p; hier werden alle Partitionen einer Zahl n mit den Elementen 1 .. p gebildet.
> partition(4);
> partition(4, 2);
> numbpart(4);
MAPLE EINFÜHRUNG - MPLINTRO 04.00a vom 14. Dezember 1998
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/m5.htm