| Galaxies in 3D |
 |
| Galaxies in 3D |
 |
In this example you will read in a file containing data of around 22,000 galaxies, convert the data to a format that can be used by Maple, write it back to a file, and then read it in again to display the galaxies in 3-dimensional space depending on their distance from the Sun.
All the Maple sheets and source files are available at the bottom of this page.
This tutorial is not intended to be complete. You should read the online help pages on the various file I/O functions. A good starting point is ?fprintf for it includes links to all other related commands (or use the help browser /Programming/Input and Output/File Manipulation).
Note: Since a much larger galaxy catalogue is available on the Net, this document has been changed in April 1999. The resulting Maple plots now show much more detail than those published before on this page.
The article mentioned above contains a plot showing that galaxies are not evenly distributed in space but that there are concentrations of galaxies in clusters forming walls billions of light years long. This plot also shows 'bubbles', vast amounts of nearly empty space with the galaxies situated on top of the bubbles.
Thanks to a catalogue of galaxies compiled and published in the Internet by John Huchra, it is possible to compute a 3dimensional plot of the galaxies with Maple using its file input and output commands. You will see `beams` not showing true structure but which are the result of exact surveys of small parts of the sky containing very dim galaxies (so-called `pencil-beam surveys`).
While the original file contains 38,909 galaxies plus a lot of data on each one, I have extracted only the necessary information (apart from the brightness data) to speed up computation. Also, all the galaxies where velocities were not available have been removed. Thus 22,746 galaxies are contained in the Maple input file.
| Data | Format (length) | Position start |
Position end |
| Name of galaxy | Alphabetic (10) | 1 | 10 |
| Right ascension - hours | Integer (2) | 11 | 12 |
| Right ascension - minutes | Integer (2) | 13 | 14 |
| Right ascension - seconds | Float (4.1) | 15 | 18 |
| Declination - sign | Alphabetic (1) | 19 | 19 |
| Declination - degrees | Integer (2) | 20 | 21 |
| Declination - minutes | Integer (2) | 22 | 23 |
| Declination - seconds | Integer (2) | 24 | 25 |
| Brightness (magnitude) | Float (5.2) | 26 | 30 |
| Heliocentric velocity | Integer (5) | 31 | 35 |
The following chart shows the position of the data and the first four lines in the file:
0 1 2 3 12345678901234567890123456789012345 ----------------------------------- 0000+0810 0000 0.0+081000 0.0028663 0000-3614 0000 3.5-361454 0.0034560 0000-3612 0000 7.5-361250 0.0014881 0000-3618 0000 9.6-361808 0.0015356For a Maple plot the names and magnitudes of the galaxies are not essential. The corresponding columns can be skipped easily using the substring function. Thus we need the data from columns
Syntax:
| Calling sequence: | readline(filename); |
| Parameter: | filename: the name of the file to be read line by line (a string) |
| Return: | the line as a string, or 0 if end of file has been reached |
We must split the resulting string into a sequence of different substrings, convert the sequence into a list by enclosing it in square brackets, and then convert each substring in the list to a numeric using parse combined with map. If the end of the file has been reached, readline returns the integer 0, so we must exit the loop reading and processing all the lines in the file using break.
So the core of the loop looks like this:
> do > alt := readline(fdread); # read in current line > if alt=0 then break fi; # if end of file, exit loop > a := map(parse, > [seq(substring(alt, i), i=[11 .. 12, 13 .. 14, 15 .. 18, > 19 .. 21, 22 .. 23, 24 .. 25, 31 .. 35])]); > # convert data to a list of numerics > [... further conversion statements ...] > od;
All the resulting numerics must be properly converted to create three-dimensional Cartesian coordinates.
The right ascension data can be converted first to degrees by
> decimal := (hrs, min, sec) -> hrs + min/60 + sec/3600;and then to radians through
> dec * 15 * Pi / 180;
A full circle consists of either 360 degrees or 24 hours (360/24=15). So the x and y Cartesian coordinates of each galaxy are:
> x := cos(dec/12*Pi);
> y := sin(dec/12*Pi);
The z ('height') coordinate is given in degrees, so:
> z := deg/180*Pi;
In 1921 Edwin Hubble discovered that galaxies are moving away from each other, and also that the more distant the galaxies the faster their motion. He found the following distance equation including the famous Hubble constant and the radial or escape velocity of the objects.
The constant's value is still not exactly known. In 1932 Edwin Hubble estimated it at being 530 km/sec/Mpc, Mpc = Megaparsec, 1 Mpc = 3.0857 *1019 km. (1 Parsec are 3.2616 lightyears or 206,264.8 AU with 1 AU the distance between the Sun and the Earth.) A new estimate for the Hubble constant was published in ASTRONOMY magazine of August '96: According to two recent studies the Hubble constant is either between 68 and 78, or between 53 and 61. Knowing the exact value is important to evaluate whether the universe is expanding forever or after a halt is contracting again. One purpose of NASA's Hubble Space Telescope is to nail down the constant more exactly.
> hubble_constant := 73*km/sec/Mpc;
> with(student): # This statement is not necessary in Maple 6 and later > equ := radialv*km/sec = hubble_constant * distance;
> isolate(equ, distance);
Thus the absolute distance is the equation above; its value is multiplied with the Cartesian x-, y-, and z-coordinates.
Syntax:
| Calling sequence: | fopen(filename, method); |
| Parameter: | filename: the name of the file to be opened |
| Return: | the file descriptor (an integer) |
As you see, fopen returns the number of the file it has opened. With all the other file I/O functions available in Maple, you may use this file descriptor instead of the complete filename.
(Note: You do not need to open the file before using fprintf, if the file fprintf has to write data to has not been opened before, fprintf does this automatically for you.)
Syntax:
| Calling sequence: | fprintf(filename or file descriptor, formatstring, sequence of variables); |
| Parameter: | filename: the name of the file to be read line by line (a string) |
| Return: | the line as a string |
Since we would like to store floats to the new file, the formatting string includes %f placeholders. Each galaxy is stored in a separate line, so the formatting string must also includes the newline tag \n for line separation. Note that the name of the file to be created is stored in the variable outputfilename, whereas the file descriptor determined by fopen is assigned to the name fdwrite which is subsequently used by fprintf.
The statments:
> outputfilename := "c:/rsinf.txt":
> fdwrite := fopen(outputfilename, WRITE); # open rsinfo for input
> do
> alt := readline(fdread); # read in current line
> if alt=0 then break fi; # if end of file, exit loop
> a := map(parse,
> [seq(substring(alt, i), i=[11 .. 12, 13 .. 14, 15 .. 18,
> 19 .. 21, 22 .. 23, 24 .. 25, 31 .. 35])]);
> # convert data to a list of numerics
> [... further statements to evaluate distance and
> Cartesian coordinates cx, cy, cz ...]
fprintf(fdwrite, "%f %f %f %f\n", distance, cx, cy, cz);
> # write coordinates to separate lines
> fi
> od;
Syntax:
| Calling sequence: | fclose(filename or file descriptor); |
| Parameter: | filename: the name of the file to be closed (a string) file descriptor: the integer returned by fopen |
| Return: | NULL |
> restart:
> galaxydata := proc(input::{string, name}, output::{string, name},
> maxdist::{integer, constant})
>
> # by Alexander F. Walz, July 1997, May 1998, December 13, 1998,
> # February 07, 1999
> local a, d, ra_decimal, decl_decimal, cx, cy, cz, alt, dist,
> dec, cartx, carty, cartz, counter, fdread, fdwrite, distance;
>
> # various functions
> dist := radialv -> 1/73*radialv; # distance of galaxies
> dec := (hrs, min, sec) -> hrs + min/60 + sec/3600;
> # conversion of sexagesimal values to decimal values
> cartx := ra -> cos(ra/12*Pi);
> # conversion of right ascension to cartesian x-coordinate
> carty := ra -> sin(ra/12*Pi);
> # conversion of right ascension to cartesian y-coordinate
> cartz := deg -> sin(deg*Pi/180);
> # conversion of right ascension to cartesian z-coordinate
>
> Digits := 7; # only in order to reduce size of output file
> counter := 0; # number of galaxies within radius Mpc
> fdread := convert(input, string);
> fdwrite := fopen(convert(output, string), WRITE);
> # open output file
> do
> alt := readline(fdread); # read in current line
> if alt=0 then break fi;
> a := map(parse,
> [seq(substring(alt, i), i=[11 .. 12, 13 .. 14, 15 .. 18,
> 19 .. 21, 22 .. 23, 24 .. 25, 31 .. 35])]);
> d := dist(a[7]);
> ra_decimal := dec(a[1], a[2], a[3]);
> decl_decimal :=
> `if`(a[4] < 0, -dec(-a[4], a[5], a[6]), dec(a[4], a[5], a[6]));
> cx := evalf(d*cartx(ra_decimal));
> cy := evalf(d*carty(ra_decimal));
> cz := evalf(d*cartz(decl_decimal));
> distance := evalhf(sqrt(cx^2+cy^2+cz^2));
> if distance < maxdist then
> counter := counter + 1;
> fprintf(fdwrite, "%f %f %f %f\n", distance, cx, cy, cz);
> # write coordinates to separate lines
> fi
> od;
> fclose(fdwrite); # close output file
> counter
> end:
galaxydata converts all the original data (first argument) of the galaxies within the given range (third
argument) and writes the new data to another file (second argument). It returns the number of galaxies
in the new file.
Syntax:
> galaxydata( > pathname of source file, > pathname of target file, > distance to Sun in Mpc); > galaxydata(`c:/data/redshift.txt`, `c:/data/rsinf.txt`, infinity);
Syntax:
| Calling sequence: | readdata(filename or file descriptor,
number of columns, 'integer'); |
| Parameter: | filename: the name of the file to be closed (a string) file descriptor: the integer returned by fopen n: number of columns, an integer (default is 1) 'integer': (optional) the name |
| Return: | a list or list of lists of numerics |
The following statements read in the file created by galaxydata, assigns the numerical data (a list of lists) to the name d, applies the map and the user-defined function f to that list in order to extract only those galaxies that are within a given distance, and finally creates a plot.
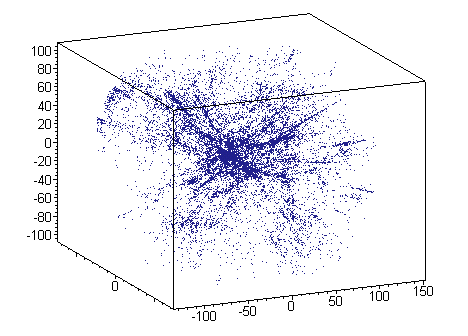
> restart: > d := readdata(`c:/data/rsinf.txt`, float, 4): > f := (x, parsec) -> `if`(x[1] < parsec, x[2 .. 4], NULL): > g := map(f, d, 150): > plots[pointplot3d](g, > symbol=POINT, color=navy, orientation=[0, 0], > axes=FRAME, scaling=constrained);The plot of the galaxies within 150 Mpc of our Galaxy:

The plot computed by Margaret Geller and John Huchra published in ASTRONOMY 08/96, p. 46:
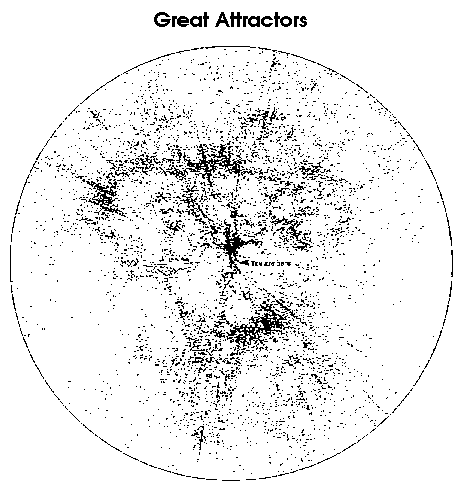
A plot in 3D clearly shows the pencil-beam surveys:
> str := plots[pointplot3d](g, symbol=POINT, color=navy, > orientation=[-24, 75], axes=BOX, scaling=constrained): > str;
> with(plottools, vrml): > currentdir(`c:/data`); # (vrml does not accept subdirectories) > vrml(str, `redshift.wrl`, emissive_color=COLOR(RGB,1,1,1));
In addition you may also download the precomputed rsinf.txt file generated by the galaxydata procedure to that you may not create the file yourself (which takes a lot of time) and also the above mentioned redshift.wrl VRML file containing all galaxies.
MAPLE UNIVERSE GALAXIES 2.0.1 current as of December 25, 2001
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mpluniv1.htm