

Reprinted with permission of Birkhauser Boston from
Maple Tech, volume 3, number 3, pp 41-47, 1996,
Tips for Maple Instructors by Robert J. Lopez.
Copyright 1996 Birkhauser Boston.
Release 4 MWS file of this article: tips2.mws (72,341 bytes).
R4 MWS files can be used in R5, as well.
In the first column of this series we addressed the question of how to present Maple as a pedagogical tool in the classroom. In addition, we described several features of Release 4 that will very likely impact the use of Maple in the classroom. In this second column of the series we again illustrate some Maple Release 4 functionality of significance in the classroom, and include a discussion of Maple styles, a feature new in Release 4.
I continue to hope this column becomes a forum where common problems can be identified and resolved, where useful hints and strategems can be found, and where pedagogical insights can be shared. Hence, I urge all readers who have their own experiences with Maple in instruction, successes and failures alike, to communicate with me by e-mail (r.lopez@rose-hulman.edu), fax(812-877-3198), or letter (Math Dept., Rose-Hulman Institute of Technology, Terre Haute, IN 47803). As much as possible, I would like this column to address real issues, from real classes. Only the column's readers can make that happen.
Match and Partial Fractions
Consider, for example, the case of partial fractions where match is an elegant way to establish an identity between two different forms of a rational function. Match will set up and solve appropriate equations for the undetermined parameters, storing the computed paremeters in a set named 's'.
> f := (5*x^2+5*x+4)/(x+1)/(x^2+1);
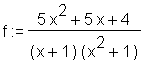
> f1 := a/(x+1); > f2 := (b*x+c)/(x^2+1);
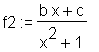
> match(f = normal(f1 + f2),x,'s');
> subs(s, f1 + f2);
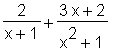
Unfortunately, match is not robust enough to support the coefficient matching needed in the method of Undetermined Coefficients from a first course in differential equations.
Match and Differential Equations
Given the differential equation,
> qq := 3*diff(y(t),t,t)+4*diff(y(t),t)+5*y(t)=cos(t);
assume a particular solution of the form
> yp := A*cos(t)+B*sin(t);
and force it to be a solution.
> qq1 := simplify(subs(y(t)=yp,qq));
This requires recognizing equation qq1 as an identity in t. However,
> match(qq1,t,'s');
Solve/identity
Thus, the student needs to learn the new syntax
> qq2:=solve(identity(qq1,t),{A,B});
a complication that could have been avoided if match were more robust or if solve/identity had been introduced initially.
Moreover, match will not identify a solution in the form
> y1 := exp(-3*t)*(5*cos(4*t) - 9*sin(4*t));
with the engineering preference
> y2 := exp(-3*t)*A*cos(4*t-phi);
Fortunately, the second approach of using solve/identity does work, provided y2 is given to Maple with the cosine term expanded. To prevent Maple from further expanding the trig terms sin(4*t) and cos(4*t) to expressions involving just powers of sin(t) and cos(t), give the expand command the additional parameter 4*t to prevent that argument from being expanded.
> q := solve(identity(expand(y1=y2,4*t),t),{A,phi});
Transfer this information to the template y2, selecting the positive value of the amplitude. This use of solve/identity performs the conversion of one form of a solution to another. It is, in fact, the simplest way to do this in Maple.
> Y2 := subs(q[1],y2);
Caution: In an early version of this calculation, I called the phase angle z instead of phi. Note the effect on y2.
> exp(-3*t)*A*cos(4*t-phi); > exp(-3*t)*A*cos(4*t-z);
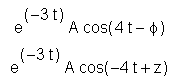
Apparently, the ordering of terms in Maple is lexicographically challenged. For the cosine function the expressions are equivalent, but when commands like expand, which rely on pattern matching, are applied, the differences in "appearance" lead to different behaviors in the ensuing calculations. This is a difficulty for authors of journal articles and classroom lessons, alike.
Two Equations in Two Unknowns
To perform the above matching by setting up and solving two equations in the two unknowns A and phi, the student has to be aware of several quirks of the expand command. First, note what happens when the equality y1 = y2 is expanded.
> expand(y1 = y2,4*t);
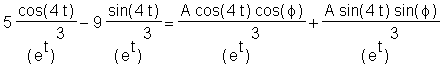
The optional parameter 4*t keeps the trig functions on the left from being expanded. If cos(4*t-z) was used, then Maple's switch of cos(4*t-z) to the equivalent cos(-4*t+z) means the trig terms on the right will not be frozen the same way they are frozen on the left.
> expand(y1 = exp(-3*t)*A*cos(4*t-z), 4*t);
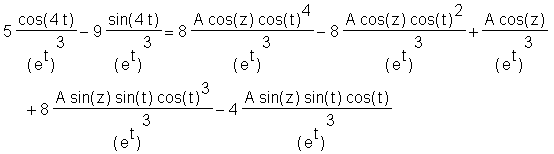
It would now take
> expand(y1 = exp(-3*t)*A*cos(4*t-z), 4*t, -4*t);
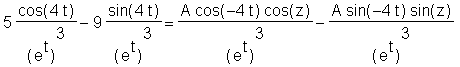
to keep all the trig terms from being expanded in terms of t. In addition, the exponential terms could be treated more conventionally. Including an exp in the expand command will force Maple to treat the exponential terms more conventionally.
> q1 := expand(y1 = y2, 4*t, -4*t, exp);
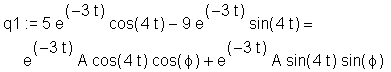
Match the coefficients of cos(4t) on both sides of the equation q1.
> e1 := map(coeff,q1,cos(4*t));
Match the coefficients of sin(4t) on both sides of the equation q1.
> e2 := map(coeff,q1,sin(4*t));
Solve equations e1 and e2 for the unknowns A and phi.
> q2 := solve({e1,e2},{A,phi});
One cure for RootOf is allvalues.
> q3 := allvalues(q2);
![[Maple Math]](maplev/tips2/tips237.gif)
Another cure for RootOf is the environment variable _EnvExplicit. Setting this variable to "true" generally suppresses Maple's use of RootOf. Thus,
> _EnvExplicit := true;
> solve({e1,e2},{A,phi});
Unfortunately, setting _EnvExplicit to "true" does not suppress all occurances of RootOf. In solving the differential equation for a body falling with quadratic drag, a problem posed as early as Calculus II, we find Maple's dsolve solution to ![]() given in terms of a RootOf containing an arctanh function, a RootOf that generates an error message when sent to allvalues. Separating variables in the ODE, and integrating both sides, leads to a transcendental equation for which solve again returns the offending RootOf. So, the use of the environment variable generally suppresses RootOf, but is not infallible.
given in terms of a RootOf containing an arctanh function, a RootOf that generates an error message when sent to allvalues. Separating variables in the ODE, and integrating both sides, leads to a transcendental equation for which solve again returns the offending RootOf. So, the use of the environment variable generally suppresses RootOf, but is not infallible.
Returning to the main discussion, we transfer the information in set q3 back into the template y2, selecting the solution with the positive value of the amplitude.
> Y2 := subs(q3[1],y2);
We have recovered the same solution found by solve/identity, but Maple's casual approach to minus signs in the argument of the cosine function causes students problems.
Finally, we show the solution with the single trig term is the same as the original y1.
> expand(Y2,4*t,exp); > ya1;
Overloading of Expand
Notice the overloading of expand. In fact, expand in Maple is used for several related, but not identical, purposes.
> expand((x+y)*(x-y));
> expand(sin(x+y));
> expand(sin(3*x));
Expand is used to clear brackets by multiplying out the product of two binomials, to apply the addition formulas in trig, and to express sin(n*x) in terms of powers of sin(x) and cos(x). But the overloading is worse than that. A fourth use of expand is to force an integral (or a sum) to demonstrate its linearity, provided the student package has been loaded.
> F := Int(a*x+b*x^2,x);
> expand(F);
With the student package loaded, expand behaves differently.
> with(student): > expand(F);
Expand and ODEs
Finally, the behavior of expand is scrutinized one last time since, in Release 4, dsolve now yields, for simple differential equations, solutions in non-standard forms.
> q := diff(y(t),t$3)-4*diff(y(t),t,t)+diff(y(t),t)+6*y(t);
> q1 := rhs(dsolve({q,y(0)=1,D(y)(0)=-1,(D@@2)(y)(0)=0},y(t)));
![[Maple Math]](maplev/tips2/tips255.gif)
It is troubling to see, in a first course in differential eqauations, a solution in such need of having its exponentials combined. Standard form can be achieved via expand,
> map(simplify,expand(q1));
but in more complex cases the overloading of expand requires extra syntax to restrain some of its latent functionality.
> q := diff(y(t),t$3)+5*diff(y(t),t,t)+17*diff(y(t),t)+13*y(t) = 0;
> q1 := rhs(dsolve({q,y(0)=1,D(y)(0)=-1,(D@@2)(y)(0)=0},y(t)));
![[Maple Math]](maplev/tips2/tips258.gif)
Here, a naive use of expand makes the expression less simple because of what happens to sin(n*x) and cos(n*x).
> expand(q1);
![[Maple Math]](maplev/tips2/tips261.gif)
Including the parameter 3*t will keep the trig functions from being expanded, and including the parameter exp will keep the exponentials from being converted to [e t] n.
> q2 := expand(q1,3*t,exp);
![[Maple Math]](maplev/tips2/tips263.gif)
The solution "in the back of the book" would have 1/et written as e(-t). That takes the additional step
> map(simplify,q2);
All together, it's
> map(simplify,expand(q1,3*t,exp));
To avoid the quirks of expand, the new functionality of collect can be exploited. Collect now takes function names for the parameter against which to collect common terms.
> collect(q1, exp);
![[Maple Math]](maplev/tips2/tips268.gif)
Of course, "textbook form" still requires
> map(simplify,collect(q1,exp));
The simplify command "uncollects" the common exponential terms, so to achieve perfect "textbook form" requires
> collect(map(simplify,collect(q1,exp)),exp);
The double collect and a map is a lot of extra syntax to have to explain to students in a first differential equations class.
We illustrate its use in computing an improper integral with the following integrand.
> f := 1/(x - 1)^(2/3);
![[Maple Math]](maplev/tips2/tips272.gif)
Notice how a naive usage results in a plot showing only part of the expected graph.
> plot(f, x = 0..3);
![[Maple Plot]](maplev/tips2/tips273.gif)
Apparently, Maple does not see the expression in f as the "cube root of a square." Instead, Maple sees it as something raised to the power 2/3.
Surd
For completeness, we remind the reader of the behavior of the nth-root function in Maple.
> simplify((-8)^(1/3));
> convert((-8)^(1/3),surd);
The surd function is ordinarily available through a readlib call, but we will invoke it by use of the convert command.
> fs := convert(f, surd);
![[Maple Math]](maplev/tips2/tips276.gif)
Conversion in the opposite direction is achieved by
> f1 := convert(fs, power);
![[Maple Math]](maplev/tips2/tips277.gif)
In this form, Maple will indeed see the expression in f1 as the "cube root of a square." In fact, the graph of f1 is the expected graph for Calculus II.
> plot(f1, x = 0..3, y = 0..10);
![[Maple Plot]](maplev/tips2/tips278.gif)
The surd function becomes less strange if we can make f1 look exactly like the original expression (by combining exponents). Hence,
> simplify(f1,symbolic);
![[Maple Math]](maplev/tips2/tips279.gif)
Plotting the surd-representation will also yield the expected graph. Additionally, the desired graph can be obtained by plotting 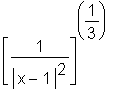 ,
, 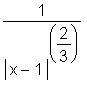 or
or 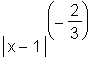 , or by typing
, or by typing 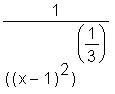 into Maple and working with the equivalent of expression f1. Maple will integrate and simplify f1, will integrate but not simplify the second and third expressions containing absolute values, and will not integrate the first expression containing the absolute value. Hence, it would be possible to avoid the surd construct in this case if due care were exercised initially.
into Maple and working with the equivalent of expression f1. Maple will integrate and simplify f1, will integrate but not simplify the second and third expressions containing absolute values, and will not integrate the first expression containing the absolute value. Hence, it would be possible to avoid the surd construct in this case if due care were exercised initially.
Integrating Surd
Maple provides the indefinite integral of the surd-representation.
> test := int(fs, x);
![[Maple Math]](maplev/tips2/tips284.gif)
To express this antiderivative in the form a calculus student would recognize, we convert back from the surd notation
> test1 := convert(test, power);
![[Maple Math]](maplev/tips2/tips285.gif)
and simplify.
> simplify(test1,symbolic);
The Improper Integral
The improper integral of interest is
> q := Int(f, x = 0..3);
![[Maple Math]](maplev/tips2/tips287.gif)
The improper integral is handled by splitting it into two integrals, each involving a limit, and each with an integrand expressed in surd-notation. We set up each of the integrals as if the small parameters a and b were positive.
> q1 := Int(fs, x = 0..1 - a);
![[Maple Math]](maplev/tips2/tips290.gif)
> q2 := Int(f, x = 1 + b .. 3);
![[Maple Math]](maplev/tips2/tips291.gif)
Evaluating each of these definite integrals,we get
> q3 := value(q1);
![[Maple Math]](maplev/tips2/tips292.gif)
> q4 := value(q2);
We are interested in the limits of these expressions as a and b each approach zero from the right.
> q5 := limit(q3, a = 0, right);
> q6 := limit(q4, b = 0, right);
The sum of these limits is the value of the improper integral.
> q7 := q5 + q6;
Cauchy Principal Value
If we were to let the parameters a and b be equal, we would compute the Cauchy Principal Value of the given improper integral.
> q8 := Int(fs, x = 0..1 - a) + Int(f, x = 1 + a .. 3);
![[Maple Math]](maplev/tips2/tips2101.gif)
Evaluating the integrals we get
> q9 := value(q8);
![[Maple Math]](maplev/tips2/tips2102.gif)
The limit as a approaches zero from the right is therefore the Cauchy Principal Value.
> q10 := limit(q9, a = 0);
Note that Maple has a built-in routine for computing the Cauchy Principal Value.
> q11 := int(fs, x = 0..3, CauchyPrincipalValue);
Once I verified that Maple is indeed an n-digit machine, I was able to see through the original difficulty I had had with the numeric differentiation results. The surprising outcome was the realization that many texts, my own included, have errors in the examples of n-digit arithmetic.
Here are the details.
Numeric Differentiation
Consider the numeric computation of f'(1) for the function f(x)=ex.
> for k from 1 to 10 do > evalf((exp(1+10^(-k))-exp(1))/10^(-k)); > od;
2.7319187
2.719642
2.71842
2.7183
2.719
2.72
2.8
3.
0
Always at a loss to explain the disappearance of digits in this calculation, I appealed to Keith Geddes for insight. "Is Maple programmed to detect the loss of significance? Does Maple intelligently deliver only those digits it knows are correct?" "No," Keith replied. "It's simply a matter of subtractive cancellation on a finite precision machine." Of course, there was an extended explanation provided by Keith, but that explanation could only be accepted if I believed that Maple was indeed behaving as a 10-digit computer. I just didn't believe that yet.
I didn't believe that, because my recollection of examples from numerical analysis texts was of discrepancies between Maple and the examples. The examples had to be revisited before this was going to be over.
Text Examples
Every numerical analysis text I've examined contains examples of 3- or 4-digit arithmetic intended to illustrate the effects of computation on a finite precision machine. My own text [1] contains, on page 183, the 3-digit example of row-reducing
> A := matrix([[-.72e-1, .3, -.21], [.874, -.267, .133], [-.501, -.123, .125]]);
![[Maple Math]](maplev/tips2/tips2118.gif)
to
![[Maple Math]](maplev/tips2/inl005.gif)
after interchanging the first and second rows. Stepping through the calculation in Maple yields
> with(linalg): Warning, new definition for norm Warning, new definition for trace > a := swaprow(A,2,1): > Digits := 3: > a1 := addrow(a, 1,2,-a[2,1]/a[1,1]): > a2 := addrow(a1,1,3,-a1[3,1]/a1[1,1]); > a3 := addrow(a2,2,3,-a2[3,2]/a2[2,2]);
![[Maple Math]](maplev/tips2/tips2120.gif)
![[Maple Math]](maplev/tips2/tips2121.gif)
The (3,3)-elements don't agree. It's tedious to check, but there is no other way to decide which version of the row reduction is correct. The arithmetic has to be checked by hand, a calculation showing the error creeps in at the last moment. The final arithmetic for the (3,3)-element is ![]() . The pivot is
. The pivot is ![]() which rounds to .993. The product of .993 and .199 is .197607 which should round to .198, leading to .201 - .198 = .003, Maple's correct result. However, if .197607 is not rounded to three places, we have the subtraction .201 - .197607 = .003393, the text's incorrect result.
which rounds to .993. The product of .993 and .199 is .197607 which should round to .198, leading to .201 - .198 = .003, Maple's correct result. However, if .197607 is not rounded to three places, we have the subtraction .201 - .197607 = .003393, the text's incorrect result.
On page 148 of [2] we find the matrix
> A := > matrix([[-.002,4.,4.,7.998],[-2.,2.906,-5.387,-4.481],[3.,-4.031,-3.112,-4.143]]);
![[Maple Math]](maplev/tips2/tips2124.gif)
row reduced, using 4-digit arithmetic without pivoting, to
![[Maple Math]](maplev/tips2/inl008.gif)
Checking this result in Maple, find
> Digits := 4; > A1 := pivot(A, 1,1,2..3); > A2 := pivot(A1,2,2,3..3);
![[Maple Math]](maplev/tips2/tips2127.gif)
![[Maple Math]](maplev/tips2/tips2128.gif)
The middle rows differ by a factor of 1000 and the last row has -10 not -11. Hand calculation shows Maple is correct. In fact, the first pivot is -2/(-.002) = 1000 so we compute
-2 - [1000(-.002)] = -2 - [2] = 0 2.906 - [1000(4)] = -3997.094 -> -3997 -5.387 - [1000(4)] = -4005.387 -> -4005 -4.481 - [1000(7.998)] = -4.481 - [7998] = -8002.481 -> -8002The second pivot is 3/(-.002) = -1500 so we compute
3 - [-1500(-.002)] = 3 - 3 = 0 -4.031 - [-1500(4)] = -4.031 + 6000 = 5.995.969 -> 5996 -4.143 - [-1500(7.998)] = -4.143 - [-11997] -> -4.143 + 12000 = 12004.143 -> 12000The third pivot is 5996/(-3997)=1.50012 -> -1.5 so we compute
5996 - [-1.5(-3997)] = 5996 - [5995.5] -> 5996 - 5996 = 0 5997 - [-1.5(-4005)] = 5997 - [6007.5] -> 5997 - 6008 = -11 1200 - [-1.5(-8002)] = 12000 - 12003 -> 12000 - 12000 = 0It is only after grinding out one of these calculations that we appreciate why errors creep in, and why the arithmetic is so rarely checked by hand. And this one error in [2] is not isolated. In fact, on the very next page of that text we find the matrix
> A := matrix([[3.02, -1.05, 2.53, -1.61], [4.33, .56, -1.78, 7.23], [-.83, -.54, 1.47, -3.38]]);
![[Maple Math]](maplev/tips2/tips2129.gif)
row-reduced, using pivoting and 3-digit arithmetic, to
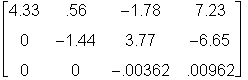
whereas Maple yields
> Digits := 3: > a := swaprow(A,2,1): > a1 := pivot(a,1,1,2..3); > a2:=pivot(a1,2,2,3..3);
![[Maple Math]](maplev/tips2/tips2131.gif)
![[Maple Math]](maplev/tips2/tips2132.gif)
The third row of Maple's a1 is correct, since we get for the pivot -.83/4.33 = -.19168 -> -.192. Then,
-.83 - [-.192(4.33)] = -.83 + [.83136] -> -.83 + .831 = .001 -.54 - [-.192(.56)] = -.54 + [.100752] -> -.54 + .108 = -.432 1.47 - [-.192(-1.78)] = 1.47 - [.34176] -> 1.47 - .342 = 1.128 -> 1.13 -3.38 - [-.192(7.23)] = -3.38 + [1.38816] -> -3.38 + 1.39 = -1.99Moreover, the third row of Maple's a2 is correct since we get for the pivot -.432/(-1.44) = .3. Then,
-.432 - [.3(-1.44)] = -.432 + .432 = 0 1.13 - [.3(3.77)] = 1.13 - [1.131] ->1.13 - 1.13 = 0 -1.99 - [.3(-6.65)] = -1.99 + [1.995] -> -1.99 + 2 = .01Wretchedly tedious as it is, I had to go through this arithmetic before I could accept Maple as an n-digit computer. My reliance on text examples was not warranted, since errors appear in them so readily. Once Maple is accepted as an n-digit calculator, the anomalous output from the numeric differentiation is easily understood.
Resolution
It is now a simple matter of subtracting 10-digit numbers to understand the numeric differentiation example. Consider, for example, the value obtained for k = 7.
> Digits := 10: > q1 := evalf(exp(1+10^(-7))); > q2 := evalf(exp(1));
q2 := 2.718281828
On a 10-digit machine, the subtraction "eliminates" seven of the digits. There are only three digits left in the mantissa of the difference.
> q1 - q2;
Of course I always understood fixed precision arithmetic. But only after I realized that Maple was truly an n-digit calculator could I see why the numeric differentiation produced the results seen above.
In Release 4 there are now named styles that can be applied to a single copy of a worksheet, converting the appearance of the worksheet on demand. However, it took me several months to begin to understand how to use "styles," and it took a call to support to discover that the "Merge Existing" button was the way to "apply" a style to a worksheet.
Since the process of "naming" a style requires using the "Save as Default" button, the very first time you experiment with naming a style you will lose the pre-sets for the style parameters. This happens so soon in the learning cycle that it generally happens before the user is even aware of it. The good folks at support tell me, however, that the default settings are "hard wired" into Maple "from the factory." When these original defaults are changed, the change is recorded, under Windows, in a file Windows/maplev4.ini. (I don't know the situation for the Mac and UNIX platforms.) In the Windows directory, this file contains various sections, one of which is the [Files] section. The original factory pre-sets can be re-established by changing, in this [Files] section, the line mentioning "Template" to read "Template=.".
In other words, you can name styles and record those styles as individual files, but the pre-set style does not have a comparable name or file corresponding. If you want to give that pre-set style a name and a standing equal to that of any other style you create and name, then before performing any experiments with styles, name and save the pre-sets as follows.
From the FORMAT menu select STYLES. The "Style Management" dialog box appears. Click the "Save As Default" button and the "Save Style Set" dialog box appears. Enter the name of a file in which the factory pre-set style is to be stored. I chose "Original.mws". There is also available in the "Save Style Set" dialog box a "Folders" section where you can choose where to save this file. (I have created a special folder of just Maple styles where I save all my named styles.) Click "OK." This returns you to the "Styles Management" window, and here, click "Done".
If you now experiment with styles and wish to revert to the factory pre-sets, you can either use the style file just created or you can edit your Windows/maplev4.ini file. I believe it is easier to use the style sheet "Original.mws" and not edit the Windows file.
Now that we have the confidence our experiments with styles can always be reversed, let's consider how to create and use an alternate style. Suppose the need is for a "projection" style with input, output, and text all black, text and input as bold, and type sizes of 12 points. Since the Toolbar contains a zoom button for magnification, the projection style need not be inherently magnified.
From the FORMAT menu, select STYLES. We'll change the characteristics of text first. In the upper left portion of the "Styles Management" window, in the panel "Styles" select "Normal." This refers to text. Click the "Modify" button. The"Paragraph Style" window opens. Click the "Font" button in the lower left portion of this window. You now have access to properties of the input font. Select "bold" and "12" and click "OK". Click "OK" on the "Paragraph Style" window.
Next, we change Maple input from red to black (and make it bold) by selecting "Maple Input" (very last item in the list) in the Styles panel. Click the "Modify" button, and make the appropriate changes in the "Character Style" window that opens. Hence, select "bold", choose the color black, and click "OK".
Finally, change the color of two-dimensional, true-math output. Select "2D Output" from the "Styles" panel and click the "Modify" button. A "Character Style" window opens from which you can select the color black. Click "OK".
All the desired choices have been made for the new style. Next, on the open "Style Management" window, click the "Save As Default" button. (I find it strange that the only way to save a style in a style file is to designate it as a default. That is why, after my initial experiments with styles, I went back and investigated how to restore the factory pre-sets. The instant you try to save your first test style you lose the pre-sets because naming a style can only be done by changing the default style.)
Just as for the process by which we created the named style "Original.mws", choose a name for the projection style, and select a folder in which to store it. Click "OK". You are again looking at the "Style Management" window. You have already changed your default style to the projection style. Even if you click the button "Revert to Default" you have changed that setting in your Windows/maplev4.int file. If you click the "Done" button, the "Style Management" window will disappear and you will be looking at a worksheet that is in the new "Projection" style.
To change the style of this worksheet back to your working style, say the factory pre-set style saved in the style file "Original.mws", choose STYLES from the FORMAT menu, then click the "Merge Existing" button on the "Style Management" window. The "Merge Existing" button opens the "Merge Styles Set" window where you can select the folder in which your style files reside, and the file name of the style you wish to apply. Make these choices, thereby selecting "Original.mws". Click "OK" and you are back at the "Styles Management" window. If you click "Done" your worksheet will appear in the factory pre-set style captured in the file "Original.mws".
But suppose you also want to restore the factory pre-sets as the default style. When you have chosen "Original.mws" from the "Merge Style Set" window, you can then click on the "Save As Default" button in the "Styles Management" window. This opens the "Save Style Set" window where you can navigate to the folder and file name of the named style you wish to set as default. When you choose these options, and click "OK", you will be told that the name already exists and do you want to over-write this file. As far as I can tell, you have to say "yes" if you want to change your default style. Finally, if you click "Done" in the "Styles Management" window, you will have changed your default style back to the factory pre-sets recorded in the "Original.mws" file created initially.
Of course, the process of applying any named style, and setting any named style as default, is the same as described above, mutatis mutandi. I did not find any of this intuitive, and had to spend a great deal of time experimenting. Perhaps those already familiar with styles from a word processor will not find managing styles as daunting as I did.
An improper integral requiring the use of the surd command for a correct rendering of 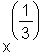 is explored. The Cauchy Principal Value is also implemented and compared to Maple's built-in CPV functionality.
is explored. The Cauchy Principal Value is also implemented and compared to Maple's built-in CPV functionality.
Numeric differentiation of ex yields an enigmatic result that only becomes transparent when Maple's behavior as an "n-digit calculator" is understood. A barrier to acceptance of Maple as such a calculator is the prevalence of errors in n-digit arithmetic in numerical analysis texts.
Finally, a discussion of creating, naming, and applying worksheet styles is given.
Author: Robert J. Lopez
Original file location: http://www.math.utsa.edu/mirrors/maple/mplrjl02.htm