

Developed by Swedish mathematician Helge von Koch in 1904, this algorithm splits a line into three parts, adds a fourth line and realigns the lines with a specific degree. p is the number of recursions and should be less than 5.
> koch := proc(p: numeric) > # SNOWFLAKE > # algorithm taken from 'Algorithmen fuer Chaos und Fraktale' > # by Dietmar Herrmann, Addison-Wesley > # original program written in BASIC > # ported to Maple V. modified and optimized by Alexander F. Walz > # Version 1.0 - July 27, 1996 > # Version 1.1 - May 23, 1999, twice as fast as v 1.0 > local m, n, k, l, s, h, x, y, pts, t, i; > h := 3^(-p); > pts := table([]): # [0, 0]; > x := 0; y := 0; > for n from 0 to (4^p-1) do > m := n; > s := 0; > for l from 0 to p-1 do > t := irem(m, 4); > m := iquo(m, 4); > s := s+irem((t+1), 3) - 1 > od; # end of for l > x := evalhf(x+cos(Pi*s/3)*h); > y := evalhf(y+sin(Pi*s/3)*h); > pts[n] := [x, y]; > od; # end of for n > [seq(pts[i], i=0 .. n-1)]; > end: > plot(koch(1), scaling=constrained, style=LINE, axes=NONE);

> plot(koch(1), scaling=constrained, style=LINE, axes=NONE);
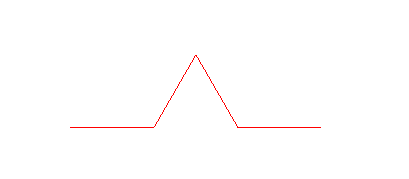
> plot(koch(2), scaling=constrained, style=LINE, axes=NONE);
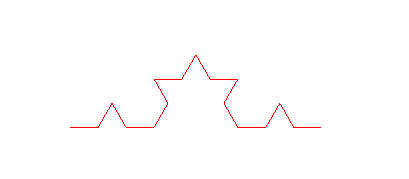
> plot(koch(3), scaling=constrained, style=LINE, axes=NONE);
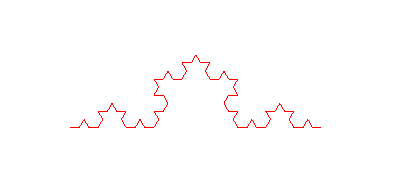
> plot(koch(4), scaling=constrained, style=LINE, axes=NONE);

> plot(koch(5), scaling=constrained, style=LINE, axes=NONE);
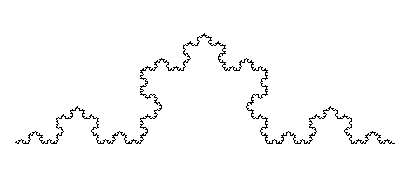
MAPLE V FRACTALS KOCHCURVE #1.1 current as of May 23, 1999
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mfrkoch.htm